Mark Coté, Project Manager, markcote@cpm.org
Whether your course assignments include CC1 or AP Calculus, the reality of teaching is that our students arrive with a diverse set of prior learning experiences and varied instructional needs. Providing universal access to the curriculum can be a daunting task; it takes time, effort and ongoing formative assessment to recognize the differences and make instructional adjustments to better meet the needs of individuals.
Can you recall your first experience with differentiation in the classroom? Mine involved two groups sorted by reading level in the second grade – the bluebirds and the red birds. Though I cannot recall’t recollect which bird I was, I do remember that each “flock” had different reading materials and remained intact throughout the entire year. I know that I was always curious about what the other kids were reading. Due to my visual impairment, I benefited from an additional accommodation; I was provided a set of large-print textbooks which were almost as big as my desktop. I was fortunate to reside in a progressive school district that recognized the necessity of instructional differentiation and provided a well-funded special education program to implement it.
So how do you differentiate to address issues of equity and access? Certainly a colorful bird approach in a mathematics classroom would simply exacerbate negative student identities and establish an additional layer of tracking to an educational system that is already fraught with countless structural obstacles. There must be a happy place between creating 150 individualized worksheets for each day of instruction and a one-size-fits-all curriculum. Indeed, there is.
The third option is to offer an engaging and enriching problem-solving experience to all students while incorporating intentional, planned differentiation during a given lesson. Equity does not mean that every student should receive identical instruction; instead, it demands that reasonable and appropriate accommodations be made as needed to promote access and attainment for all students” (NCTM, 2000, p. 12). Such “reasonable and appropriate accommodations” have been the research interest of Dr. Carol Ann Tomlinson (William Clay Parrish Jr. professor and chair of educational leadership, foundations, and policy at the University of Virginia’s Curry School of Education) for several decades. Dr. Tomlinson has observed and studied schools in which the entire faculty focused on providing a third condition: differentiation in mixed-ability classrooms where regular planning for a full spectrum of learners—including advanced learners—was a given. She reports that, “Teachers in those schools typically ‘”taught up,’” planning first for advanced learners, then scaffolding instruction to enable less advanced students to access those rich learning experiences. Further, they extend the initial learning opportunities when they are not sufficiently challenging for highly advanced learners. In those schools, achievement for the full spectrum of learners—including advanced learners—rose markedly when compared to peer schools where this approach was not pervasive.”
This “full spectrum” option has gained traction in many CPM classrooms. While the number of possible instructional adjustments is infinite, there exists a common pedagogical thread. Productive differentiation begins with the belief that every student can learn the mathematics in the course and that every teacher is capable of improving learning outcomes for their students. Next, culture-building activities help establish an environment of inclusion and encourage students to take personal responsibility for their learning. Teachers model and impart a growth mindset attitude, persistence in the face of adversity, and the value of learning from one’s mistakes. Finally, specific lesson adjustments require anticipation of struggle, data gathering through formative assessment, planning and execution. The following four examples of differentiation address the instructional components of the daily lesson, chapter closure, homework, and assessment.
Further Guidance
Teacher Researcher Angie Kraft, a veteran member of CPM’s Teacher Research Corps (TRC), has spent the past couple of years investigating the process of adjusting course content to increase accessibility.
Our district has spent a lot of time having special education teachers plan with regular education teachers to build scaffolds for one to two core problems for each lesson,” reports Kraft. “These scaffolds are developed carefully to meet specific student needs without a loss of rigor; the goal is to allow every student access to the math regardless of ability level.
She provided the following Core Connections, Course 1 problem as an example:

“The teachers collaborated to create a tool to help students visualize the learning target. A generic rectangle was drawn as a graphic organizer so that the students would have an idea about where to put in the values 8, 30, and 2. Then, some used a calculator to find the products inside the rectangle,” Kraft explained.

“This way, more students were able to access the same material and fully participate with the team. The only drawback was the amount of planning time required as these scaffolds are specific to a given lesson and need. However, the longer we do CPM, the more resources we have developed, stored, and shared among each grade level,” she concluded.
Closure Stations
Teacher Leader and Teacher Researcher Jennifer McCalla has participated in practitioner inquiry with the TRC since 2015. McCalla’s research interests have included student self-assessment and study team improvements. In her TRC white paper entitled Do Your Students Know What They Don’t Know, McCalla explains how she and her team developed learning target trackers and student self-assessment tools to investigate the impact of engaging students in metacognitive behavior. To prepare for a chapter assessment, McCalla created closure stations for each chapter to serve as a self-directed review. Each table in the classroom focused on a different learning target (typically there were 6 – 7 learning targets for a given test) and had the learning target sign on the table with corresponding practice problems and an answer key for the practice problems (example below).

McCalla explained the process. “Before they started the closure stations, students were asked to prioritize the learning targets being tested and number them from weakest to strongest. Then they visited the closure station tables in that order. This was the first time that the students would not be completing the closure stations with their teams, rather visiting the stations based on their prioritized weaknesses. This was a great way to differentiate their learning and practice based on their past performance. Normally, what I (and many teachers) reviewed in class was at the discretion of the teacher, not the students. This helped the students narrow their focus for studying while reflecting on their strengths and weaknesses. Completing the closure stations allowed all students the opportunity and experience of becoming their own agents for improving their understanding.” An example of a student rating sheet follows.
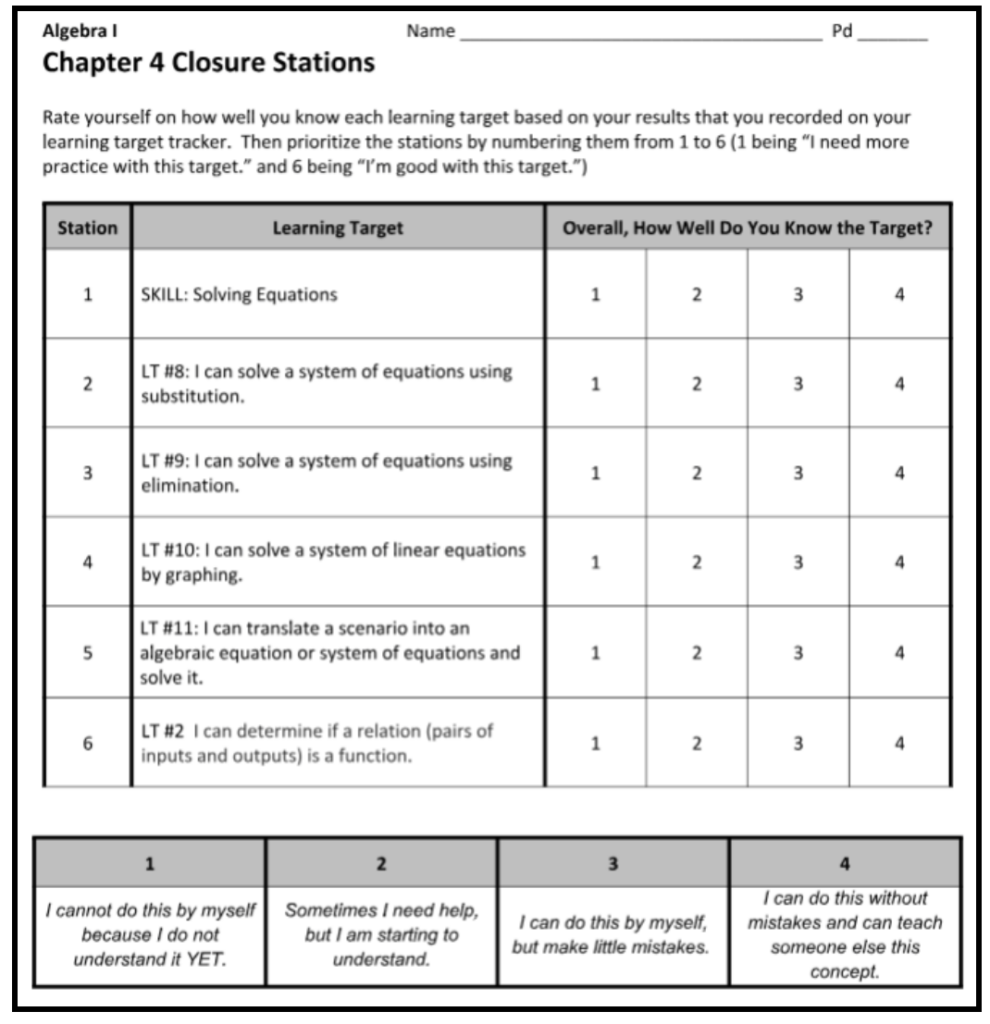
McCalla reported that the students loved the closure stations and, surprisingly, did not follow their friends to the stations, but rather visited in the order in which they rated themselves. They also appreciated knowing which learning targets would be the focus for the upcoming test. Before the next chapter test, the students were begging McCalla to have closure stations and these became a staple in the classroom. An interesting side effect of having the students prioritize their learning targets was that McCalla was physically able to see what learning targets the students needed the most support in when they were asked to go to the station that they set as their first priority.
Traffic Lights
In conjunction with the ongoing formative assessment that occurs during a lesson, many teachers employ opportunities for differentiation using the Review & Preview problems; the emphasis of each set can be adjusted to challenge more advanced learners and to support students who need more work with the fundamental skills and core ideas. CPM Coach and Teacher Leader Tracy Frank learned of a “traffic lights” strategy from several teachers in Wisconsin who were struggling to get their students to try and/or complete any of the assigned problems. Prior to making an assignment, the teachers carefully selected problems from the set that supported the learning intentions, either reinforcing the lesson, reviewing previous material, carrying previously learned concepts into more complex situations or to deeper levels, previewing upcoming material, teaching a simple concept not covered in a lesson, or providing an enrichment opportunity.

Frank explains, “As the assignment was made, selected problems were labeled as either green light, yellow light or red light. Students were taught that the green light problems were mandatory review exercises considered accessible to all students. Yellow light problems were typically extensions of the day’s lesson or a preview of forthcoming material.” Though recommended, the yellow light problems were optional to all. In some cases, students were given the choice of exchanging the green light problems for the yellow if they felt that they knew the green light material well. Red light problems, typically with an extension or enrichment focus, were also optional.
To date, a number of Teacher Researchers have tried the traffic lights strategy and reported that providing a choice to modify the length of a homework assignment was empowering for the students and resulted in increased engagement in the Review & Preview process.
Test Correction Teams
Teacher Leader and Teacher Researcher Heather Thacket developed a new idea for differentiation when tests were returned to her students. She found it impossible to meet with every individual student as they corrected their tests – so many questions with so little time! So Thacket created temporary test correction teams based on test results. Each team was comprised of one member who truly struggled, one or two students who did okay, and one member who had demonstrated mastery. All problems were graded using a 4 point rubric and any problem that was scored below a 4 was required to be corrected and submitted for additional credit, so it was a rare occurrence when a particular student had no correcting to do.
Thacket reports, “This works well if you have been using study team teaching strategies all along. The kids are constantly regrouping during the daily lessons, so there is no stigma attached to this particular move following a test. The fact that each team has a leader that can serve as a resource really frees me up to check-in more with each team. I can also get information about common concerns and decide when direct instruction is needed.”
The test correction teams disperse at the end of the period and complete a correction analysis form the following day. Thacket is so happy that she made a change to this part of the assessment process. She states, “Doing this gives them more ownership of their test results and they are more actively engaged in learning from their mistakes. They tell me that they enjoy the opportunity to discuss the work with their peers and fix errors in small groups.”
Differentiation begins with the mindset that the primary objective of mastering essential mathematical knowledge, concepts, and skills remains the same for every student. As we have seen, teachers may use different instructional methods to help students meet those expectations by incorporating further guidance, temporary regrouping and student choice. And no one needs to be a bluebird or a red bird.

