CPM Educational Program provides both
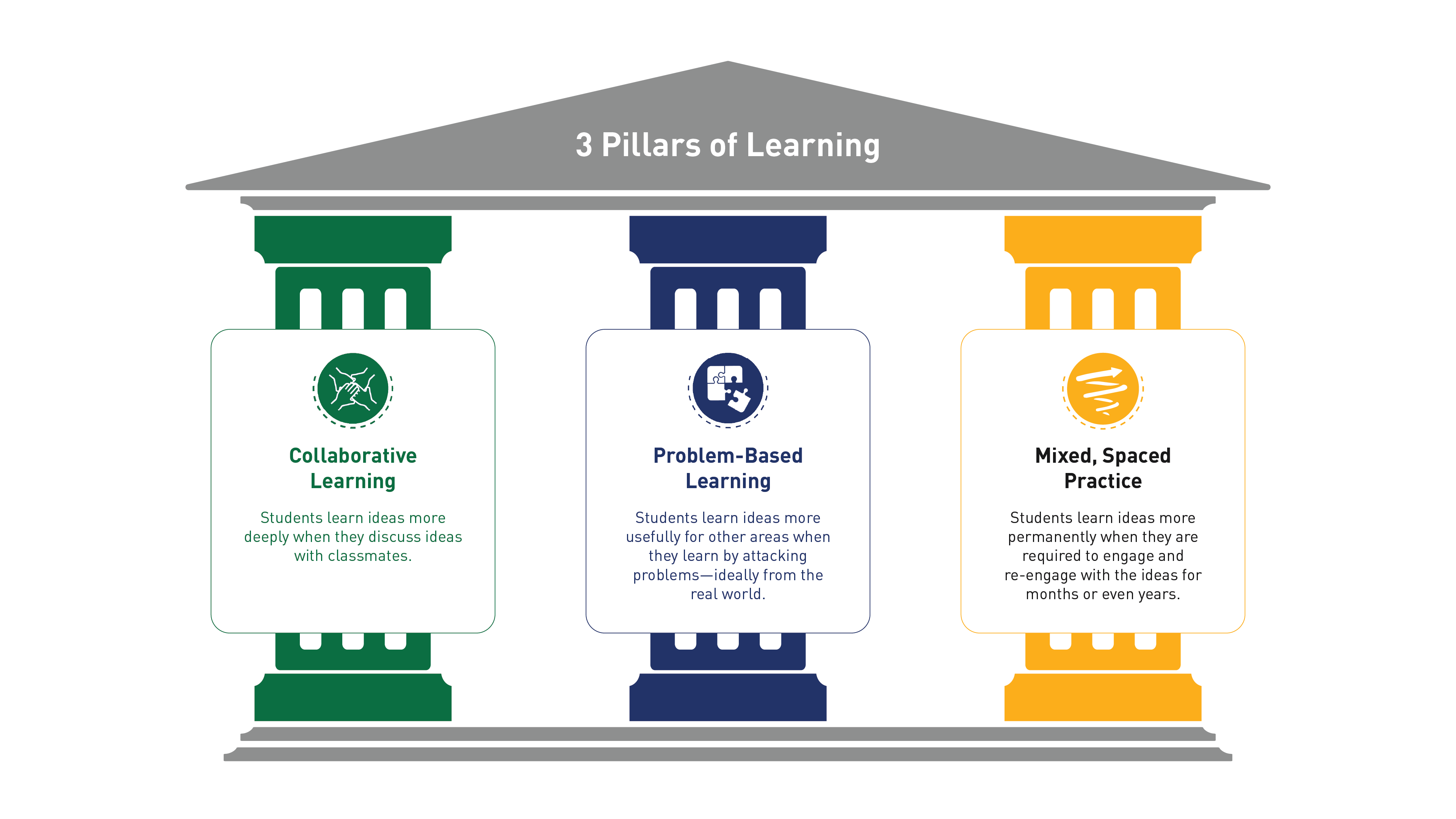
*These pillars are reflected in current NCTM standards and research in mathematics education; what we know about their benefits for mathematics learning continues to deepen and expand but not shift.
Read the 2023 CPM Research Base Report (PDF)
Read the 2013 CPM Research Base Report (PDF)
Read the Original CPM Research Base Report (PDF)
CPM Educational Program, a California non-profit corporation, has provided problem-based instructional materials and professional development for teachers since its inception in 1989. CPM teaching strategies focus on how students best learn and retain mathematics. The research-based principles that guide the course are the following:
I really like the way that this works because all the lessons make me do stuff I didn’t know before and then we do it a lot more often. Basically I learn it ahead of time before what we do in math class. Also it helps keep my math grade up because I learn new things.
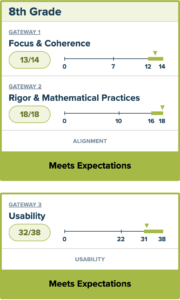
Read the complete EdReports Publisher Commentary for Core Connections, Courses 1-3 (PDF) and CPM’s response.
We invite you to read highlights from Ed Reports.org review of CPM Middle School Core Connections, Courses 1-3 (PDF).
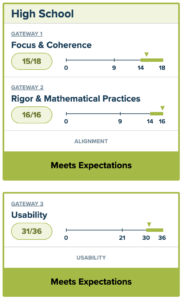
We invite you to read the complete CPM Integrated Series EdReports review.
© 1989-2023 CPM EDUCATIONAL PROGRAM All rights reserved. CPM Educational Program is a 501(c)(3) educational nonprofit corporation.
0.1.1
Who are my classmates?
0.1.2
How do I work collaboratively?
0.1.3
What questions can I ask?
0.1.4
How can I categorize my words?
0.1.5
How can I communicate my ideas?
0.1.6
How can the team build this together?
0.1.7
What do we need to work togethe
1.1 Numbers and Data
1.1.1 How should data be placed on this line?
1.1.2 Where do these numbers belong on this line?
1.1.3 How can I use two lines to solve problems?
1.1.4 How can data be used to answer a question?
1.1.5 How are histograms helpful?
1.1.6 How else can data be displayed?
1.2 Shapes and Area,
1.2.1 How can I write equivalent expressions in area and perimeter?
1.2.2 What shapes make up the polygon?
1.2.3 How can I make it a rectangle?
1.3 Expressions
1.3.1 How can I describe it using symbols?
1.3.2 What are the parts of an expression?
1.3.3 How do I work with decimals?
1.3.4 How do I multiply multi-digit decimals?
1.3.5 How can I represent the arrangement?
2.1 Ratio Language
2.1.1 How can I compare two quantities?
2.1.2 How can I write ratios?
2.1.3 How can I see ratios in data representations?
2.2 Equivalent Ratios
2.2.1 How can I visualize ratios?
2.2.2 How can I see equivalent ratios in a table?
2.2.3 How can I see equivalent ratios in a double number line?
2.2.4 How can I see equivalent ratios in tape diagrams?
2.2.5 How can I use equivalent ratios?
2.2.6 What do these represent?
2.3 Measurement
2.3.1 What are the measurements?
2.3.2 What are the units?
2.3.3 How can I convert units
3.1 Measures of Center
3.1.1 How can I measure the center?
3.1.2 How else can I measure the center?
3.1.3 Which is the better measure of center?
3.1.4 What happens when I change the data?
3.2 Integers
3.2.1 What numbers do I see?
3.2.2 What number is this?
3.2.3 What does a number line say about a number?
3.2.4 How do I compare different types of numbers?
3.3 Absolute Value
3.3.1 How do I describe the location?
3.3.2 How far do I walk?
3.3.3 Which one is greater?
3.3.4 How do I communicate mathematically?
3.4 Coordinate Plane
3.4.1 How can you precisely indicate a location?
3.4.2 What is the correct order?
3.4.3bWhat symbol represents me?
4.1 Fractions, Decimals, and Percents
4.1.1 How can I tell if the ratios are equal?
4.1.2 What does “percent” mean?
4.1.3 How can I convert a fraction?
4.1.4 How can I convert a percent?
4.1.5 How can I convert a decimal?
5.1 Variation in Data
5.1.1 How do I ask a statistical question?
5.1.2 What does each representation say about the data?
5.1.3 What does the box in a box plot represent?
5.1.4 How else can I describe data?
5.2 Area
5.2.1 What is the height?
5.2.2 Can I reconfigure a parallelogram into a rectangle?
5.2.3 How do I calculate the area?
5.2.4 How many triangles do I need?
5.2.5 What is my perspective?
5.2.6 Is it fair to play by the rules?
5.2.7 What shapes do I see?
5.3 Fractions
5.3.1 How can I represent fraction multiplication?
5.3.2 How can I multiply fractions?
5.3.3 How can I multiply mixed numbers?
6.1 Rules of Operations
6.1.1 What does it mean?
6.1.2 What do mathematicians call this?
6.1.3 How much should I ask for?
6.1.4 How can I write mathematical expressions?
6.1.5 How do mathematicians abbreviate?
6.1.6 In what order should I evaluate?
6.2 Multiples and Factors
6.2.1 When will they be the same?
6.2.2 What are multiples?
6.2.3 What do they have in common?
6.2.4 Who is your secret valentine?
6.2.5 How can I understand products?
6.2.6 How can I rewrite expressions?
6.2.7 Which method do I use?
7.1 Whole Number and Decimal Division
7.1.1 How can I share equally?
7.1.2 Which strategy is the most efficient?
7.1.3 How can I write the number sentence?
7.1.4 How can I divide decimals?
7.1.5 How should the problem be arranged?
7.2 Fraction Division
7.2.1 What if the divisor is a fraction?
7.2.2 How many fit?
7.2.3 How can I visualize this?
7.2.4 What is common about this?
7.2.5 How can I use a Giant One?
7.2.6 Which method is most efficient?
8.1. Algebra Tiles
8.1.1 What do these shapes represent?
8.1.2 What does a group of tiles represent?
8.1.3 What is an equivalent expression?
8.1.4 Which terms can be combined?
8.1.5 What do the numbers mean?
8.1.6 What can a variable represent?
8.2 Expressions
8.2.1 How can I count it?
8.2.2 What if the size of the pool is unknown?
8.2.3 How can I use an algebraic expression?
8.3 Equations and Inequalities
8.3.1 Which values make the equation true?
8.3.2 How can patterns be represented?
8.3.3 What is the equation?
8.3.4 How many could there be?
1.1 Data and Graphs
1.1.1 How can I represent data?
1.1.2 How can I use data to solve a problem?
1.1.3 Is the roller coaster safe?
1.1.4 Is there a relationship?
1.1.5 What is the relationship?
| 8.1 | Introduction to Functions | |
| 8.1.1 | How can you (de)code the message? |
| 8.1.2 | How can a graph tell a story? |
| 8.1.3 | What can you predict? |
| 8.1.4 | Which prediction is best? |
| 8.1.5 | How does the output change based on the input? |
| 8.1.6 | How do you see the relationship? |
8.2 | Characteristics of Functions | |
| 8.2.1 | What is a function? |
| 8.2.2 | How can you describe the relationship? |
| 8.2.3 | How do I sketch it? |
| 8.2.4 | How many relationships are there? |
8.3 | Linear and Nonlinear Functions | |
| 8.3.1 | Is it linear or nonlinear? |
| 8.3.2 | What clues do ordered pairs reveal about a relationship? |
| 8.3.3 | What other functions might you encounter? |
| 9.1 | Volume | |
| 9.1.1 | Given the volume of a cube, how long is the side? |
| 9.1.2 | What if the base is not a polygon? |
| 9.1.3 | What if the layers are not the same? |
| 9.1.4 | What if it is oblique? |
| 9.1.5 | What if it is a three-dimensional circle? |
9.2 | Scientific Notation | |
| 9.2.1 | How can I write very large or very small numbers? |
| 9.2.2 | How do I compare very large numbers? |
| 9.2.3 | How do I multiply and divide numbers written in scientific notation? |
| 9.2.4 | How do I add and subtract numbers written in scientific notation? |
| 9.2.5 | How do I compute it? |
9.3 | Applications of Volume | |
| 9.3.1 | What does a volume function look like? |
| 9.3.2 | What is the biggest cone? |
| 9.3.3 | How do all the items fit together? |
| 10.1 | Explorations and Investigations | |
| 10.1.1 | How close can I get? |
| 10.1.2 | Can you make them all? |
| 10.1.3 | How many triangles will there be? |
| 10.1.4 | What’s my angle? |
| 10.1.5 | Function-function, what’s your function? |
| 10.1.6 | Is it always true? |
| 10.1.7 | What’s right? |
| 10.1.8 | What’s your story? |
This professional learning is designed for teachers as they begin their implementation of CPM. This series contains multiple components and is grounded in multiple active experiences delivered over the first year. This learning experience will encourage teachers to adjust their instructional practices, expand their content knowledge, and challenge their beliefs about teaching and learning. Teachers and leaders will gain first-hand experience with CPM with emphasis on what they will be teaching. Throughout this series educators will experience the mathematics, consider instructional practices, and learn about the classroom environment necessary for a successful implementation of CPM curriculum resources.
Page 2 of the Professional Learning Progression (PDF) describes all of the components of this learning event and the additional support available. Teachers new to a course, but have previously attended Foundations for Implementation, can choose to engage in the course Content Modules in the Professional Learning Portal rather than attending the entire series of learning events again.
