Karen Wootton, Director of Assessment
My new mission, along with changing the perception of mathematics and math teaching in the U.S. within my lifetime, is to eradicate the use of the word “find” from mathematics. This mission formulated slowly; in fact, I spent the first 20 years of my career using the term freely. “Find x” was definitely part of my lexicon as was “Find the width,” “Find the area,” “Find the distance”. I used it all the time.
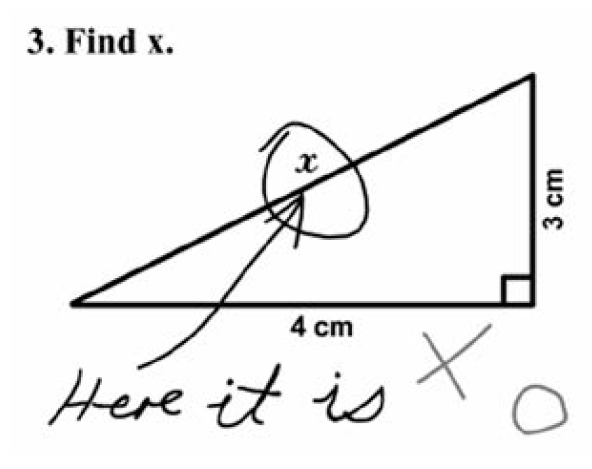
Maybe it was the well-circulated comic that had me questioning my practice and pushed me towards this mission. At first I just made it a personal goal to not use the “F” word in math problems that I wrote, but now I have formulated my opinion on why I must rid the math world of “find.” Some people might dismiss the comic as just the response of a smart aleck student, and not worthy of extra clarification. I strongly disagree with that and will now explain why we must be more clear with our language.
This is a bigger problem than thwarting smart alecks. Let’s remind ourselves of one of our Standards of Mathematical Practice: attend to precision. Is it really precise to say “Find x”? What does that ask the student to do? In particular, what does that tell the struggling student to do?
The definition of “find” is “to discover or perceive by chance.” Is that how you want your students to think that is how we do math? Do you want them to think of solving math problems as random, or by chance? For many students, and in particular, struggling students, most of their confusion stems from not seeing the connections, and think that most of math is random. To many struggling students, math is for the lucky who are good guessers of what to do next, or for those people with the elusive math gene that enabled them to be “math people.”
Let us explicitly ask students what it is we want or expect. Rather than “Find the intercepts” which implies that there is some way to just have them appear before you, change this to “What are the intercepts?” Asking the question at least implies there is something for the reader to do rather than rely on chance. Better yet, “Calculate the intercepts” or “Determine the intercepts.” If we ask “Find the intercepts” we must give full credit to the student that draws arrows pointing to the intercepts on the graph because the student has accomplished exactly what was asked. But, if that is what you want students to do, why not say “Point to the intercepts on the graph”? If we expect our students to attend to precision, we must model what that looks like. Even if we are asking something that might have an element of luck, we can do better than “find.” “Find a strategy” can be replaced with “Develop a strategy” or “Create a strategy” which implies there could be creative work, but work none the less.
So here is your challenge: whenever you are writing a math problem and are about to type the “F” word, reconsider. Can you turn a find-statement into a more precise question? Can you write the question as precisely as possible, to be sure your expectations are clear? Let us stop the perception that math is done by chance.

