
Fraction Feud is a card game in CPM’s 8th grade support course Inspirations & Ideas. Fraction Feud cards were developed to engage students with fractions in ways they may not have experienced before. In a Fraction Feud deck, there are 13 different fractions represented in 4 different operations (+, -, ×, ÷) for a total of 52 cards. The fraction of area shaded on a card is that card’s value.
Fraction Feud cards are really great. They are ripe with opportunities to reason about unit fractions, equivalent fractions, magnitude, partitioning ... everything we want them reasoning about, instead of trying to rely on procedures.
The kids absolutely loved Fraction Feud War, and they were really sad the class ended.
Students enjoy getting to play a game, and they were really engaged. It was good practice for them to find what fractions the cards represent and then compare them.
The Fraction Feud cards are awesome! Students have such a negative view of fractions. Trying to use them in a game is a great way to focus their thinking. Fraction Feud cards are really great. They are ripe with opportunities to reason about unit fractions, equivalent fractions, magnitude, partitioning ... everything we want them reasoning about, instead of trying to rely on procedures.
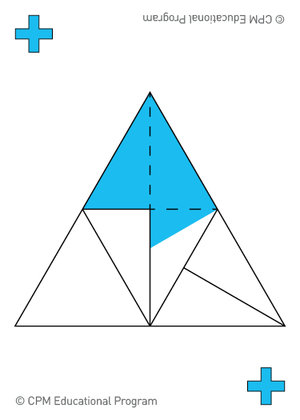
Fraction Feud War: (2 players) Deal all of the Fraction Feud cards face down to yourself and a partner so that each player has half the deck. Each player places their pile of cards face down in front of them. Play begins when each player turns over the top card in their pile at the same time and places it face up in the center of the table. The owner of the card with the greatest fraction of area shaded wins that round and takes both cards and places them at the bottom of their pile. If the two cards are equivalent, this means war! Each player then places one card face down and the next card face up for a total of six cards in play. The player whose last card has the greatest fraction of area shaded wins the war. All six cards are collected by the winner and placed at the bottom of their pile. Then play resumes. The game is over and the war is won when one player has all of the cards in the deck.
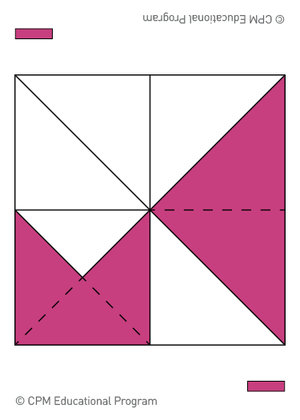
Slap <⅜: (2 or more players) Deal all of the Fraction Feud cards face down evenly between each player. Without looking at any of the cards, each player makes a neat pile in front of them. Extra cards are placed face up in a center pile. Players take turns placing their top card face up in a center pile. If the fraction of area shaded on the top card in the center pile is less than ⅜, the first player to slap the card and correctly state the fraction represented on the card moves the center pile to the bottom of their pile. If the card is slapped and the fraction is greater than or equal to ⅜, or if the player misidentifies the fraction, the first player to correctly identify the fraction takes the center pile. Players must shuffle the cards in their pile after taking the cards from the center pile. The player with the most cards after a set amount of time wins the game.
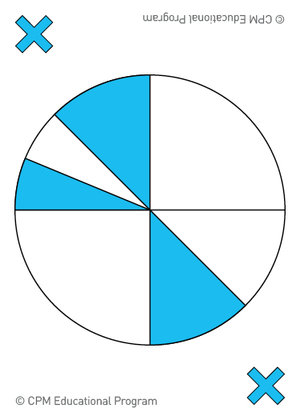
Go Fish Fractions: (2 to 5 players) Deal seven cards to each player when playing with 2 or 3 players. Deal five cards to each player when playing with 4 or 5 players. The remaining cards are spread out face down in the center. Players take turns asking for a specific fraction in order to make pairs of equivalent cards. If the player who is asked has the fraction, they surrender that card to the asking player. If the asked player does not have the fraction, the asking player must “Go Fish” in the center pile. When an equivalent pair is made it is removed from play and held for scoring. The player with the most equivalent pairs after all of the cards are used wins.
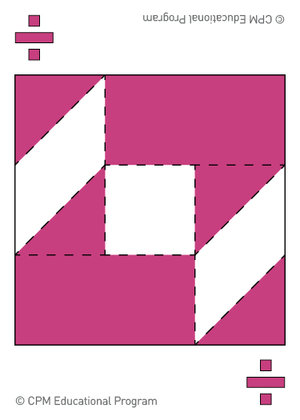
Fraction Concentration: (2 or 3 players) Shuffle the Fraction Feud cards and then lay them out face down in six or seven rows. Players take turns flipping two cards trying to find two cards that match. Cards match when the image and the color of the image are the same. When two cards match, the player must name the fraction of area shaded on the card before claiming the pair. When a player correctly claims a matching pair, they can continue to flip two cards, searching for additional pairs until they are unsuccessful. If they incorrectly name the fraction, another player can steal the pair by naming the fraction correctly. The player with the most pairs after all cards have been claimed is the winner. Half the deck (26 cards of the same color) can be used if there are only two players.
Last Fraction Standing: (4 or more players) Deal all of the Fraction Feud cards out to the entire class. Depending on the size of your class, some players may have fewer cards than others. Players can look at their cards and choose the initial order. Allow players to move around the room to find a partner. When the players each find a partner, they play a round of Fraction Feud War with a “spin.” In this case, the player who wins takes all of the cards from the other player. After surrendering their cards, the losing player sits down. The winning player then shuffles all of their cards without intentionally manipulating the order in any way. If a player with one card happens to tie with a player who has more than one card, the player with more cards will turn up their second card to break the tie. If two players who each have one card tie, they shake hands and move on. Each rotation of Fraction Feud War must be monitored. If not, a player could intentionally skip a round to improve their chances of being the last person standing with Fraction Feud cards. If an odd number of players are partnered up, the same principles of Fraction Feud War apply.
WODB: Turn four different cards face up. Choose which card among the four that does not belong with the others and justify why it does not belong.
Operations: Turn two cards face up. Determine the value of each card. Perform the operations shown on each card with the fractions.
Fraction Sort: Separate one operation (+, -, ×, ÷) from the deck. Arrange the 13 cards of that operation in ascending order based on their values.
Do you have a new way to use the Fraction Feud cards? Please submit your idea(s) to intervention@cpm.org for consideration.

This professional learning is designed for teachers as they begin their implementation of CPM. This series contains multiple components and is grounded in multiple active experiences delivered over the first year. This learning experience will encourage teachers to adjust their instructional practices, expand their content knowledge, and challenge their beliefs about teaching and learning. Teachers and leaders will gain first-hand experience with CPM with emphasis on what they will be teaching. Throughout this series educators will experience the mathematics, consider instructional practices, and learn about the classroom environment necessary for a successful implementation of CPM curriculum resources.
Page 2 of the Professional Learning Progression (PDF) describes all of the components of this learning event and the additional support available. Teachers new to a course, but have previously attended Foundations for Implementation, can choose to engage in the course Content Modules in the Professional Learning Portal rather than attending the entire series of learning events again.
The Building on Instructional Practice Series consists of three different events – Building on Discourse, Building on Assessment, Building on Equity – that are designed for teachers with a minimum of one year of experience teaching with CPM instructional materials and who have completed the Foundations for Implementation Series.
In Building on Equity, participants will learn how to include equitable practices in their classroom and support traditionally underserved students in becoming leaders of their own learning. Essential questions include: How do I shift dependent learners into independent learners? How does my own math identity and cultural background impact my classroom? The focus of day one is equitable classroom culture. Participants will reflect on how their math identity and mindsets impact student learning. They will begin working on a plan for Chapter 1 that creates an equitable classroom culture. The focus of day two and three is implementing equitable tasks. Participants will develop their use of the 5 Practices for Orchestrating Meaningful Mathematical Discussions and curate strategies for supporting all students in becoming leaders of their own learning. Participants will use an equity lens to reflect on and revise their Chapter 1 lesson plans.
In Building on Assessment, participants will apply assessment research and develop methods to provide feedback to students and inform equitable assessment decisions. On day one, participants will align assessment practices with learning progressions and the principle of mastery over time as well as write assessment items. During day two, participants will develop rubrics, explore alternate types of assessment, and plan for implementation that supports student ownership. On the third day, participants will develop strategies to monitor progress and provide evidence of proficiency with identified mathematics content and practices. Participants will develop assessment action plans that will encourage continued collaboration within their learning community.
In Building on Discourse, participants will improve their ability to facilitate meaningful mathematical discourse. This learning experience will encourage participants to adjust their instructional practices in the areas of sharing math authority, developing independent learners, and the creation of equitable classroom environments. Participants will plan for student learning by using teaching practices such as posing purposeful questioning, supporting productive struggle, and facilitating meaningful mathematical discourse. In doing so, participants learn to support students collaboratively engaged with rich tasks with all elements of the Effective Mathematics Teaching Practices incorporated through intentional and reflective planning.