Dan Henderson, Millington, MD, DanielHenderson@cpm.org

I’ve been thinking about how to normalize students changing their minds in math class. The way I see it, you have to change your mind to learn. That’s, like, what learning is. I mean, I’ve heard Daniel Willingham misquoted as saying that learning is the residue of thought, but that’s memory. Memory is the residue of thought. Learning is letting your ideas and conceptions evolve. So I’ve been thinking about how to normalize the evolution of ideas in math class.

How can I consistently cultivate kaizen (constant improvement) in my students? I have made a few steps in that direction, but no game-changers. I’ve shown videos praising the elasticity of brains; displayed slogans like “Every expert was once a beginner” and “Mistakes are expected, inspected, and respected;” and preached the power of “yet” on several occasions. But how can I move beyond slogans and one-off interventions toward perpetual progress?

I’m always tempted to declare “Everything is hopeless” at this time of year, but the truth is, it’s not. Though it is dark outside, our future is bright. We can do several things to normalize changing minds in math class. Here are a few within our power:

• Present specialized problems. Take the first few minutes of class to invite students to change their responses several times in a row with a slow reveal, encourage students to generate insights through trial and error in a dakabibi*, or work out a definition by considering examples and non-examples.
  
• Work on erasable surfaces. Say, “Consider changing your plan” by having students work on whiteboards, chalkboards, windows, laminated paper, sheet protectors, or repurposed shower curtains.
  
• Invite metacognition. Prompt students to revisit ideas and conceptions with journal prompts, self-assessments, and rubrics that provide feedback instead of a grade. Provide plenty of white space in notes for students to annotate solutions and record their own takeaways.
  
• Implement routines. Structure as many interactions as you can around iteration and revision. Call out Rough Draft Talk, use language routines like Stronger and Clearer each time, and incorporate talk moves to help students build on and modify ideas even if they don’t have their own starting point.
  
• Use teacher moves. Reframe changing your work as a positive move forward. Ask students to estimate first or give wrong answers only. Bring students into an evolving problem landscape by launching tasks orally and introducing constraints as they come up naturally. Model changing your mind by making declarative statements and having students talk you out of them. Lower the stakes by having students discuss with partners.
  
• Position all contributions as helpful. Amplify contributions of all types, including those made by students’ gestures, pictures, and phrases borrowed from other languages. Make visible how all students’ representations connect. We need to go beyond labeling ideas as “brilliant” and “wrong” and recognize that student responses most often represent their best understanding given their current model and information. It is not a misconception, but rather their at-the-moment conception based on their knowledge. Connect misdirected, circuitous, and partial solutions to the learning goal during lesson consolidation. Encourage students to learn from each other using Swapmeet and Stop and Scan (or I Spy) strategies. Say things like, “Sasha, can you share what you said to your team with the class? I thought that was really helpful.”
  
• Control our own reactions. Focus students on the process, not the answer. Students need affirmation, not answers; they are often more in need of encouragement than help. Listen to what students say and ask them about it. Respond to questions with questions that push students to think deeper about the problem. Don’t be afraid to leave some questions unanswered.

Constant improvement in nature is commonplace, conventional, and even necessary. It is natural that things and ideas evolve. We should anticipate change and growth every day. My quest to renormalize changing minds does not go against the natural grain of learning. Rather, it puts a nice finish on it to protect and accentuate the natural beauty of that process. Each suggestion above moves us in the right direction, and collectively they send a powerful message about what we value.

And that is just a few of the things we can do. I am proud to say that the Inspiring Connections courses (available now, ask your Regional Professional Learning Coordinator and/or attend the Inspiring Connections session at CPM’s National Teacher Conference!) include all this and much more. So, that’s what I’ve been thinking. What are your thoughts? How are you normalizing iteration, evolving ideas, and kaizen?

*Dakabibi™ refers to a puzzle with a set of numbers and several empty boxes that need to be filled while meeting certain conditions. For example, using the digits 0 through 9 at most once each, arrange the digits to create a true equation.

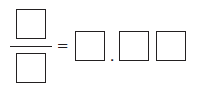
[ Responses may vary. For example, _ 1/4 = 0 .25, _ 3/4 = 0.75, or _6/5 = 1.20. ]

The term Dakabibi comes from the Twi phrase “adaka a bibiara ?ni mu,” which translates literally to “a box that everything is not inside.” This phrase is shortened to Dakabibi in CPM courses. Twi is a language spoken in Ghana and is one of the more widely used of over 50 languages spoken there. Like other West African languages, Twi is a tonal language; it has several phonemes that are very difficult for non-native speakers to pronounce. Almost a third of the Ghanaian population speaks Twi as a first or second language. Twi is not the most-spoken language in Ghana, but it is the most-spoken language by Ghanaians in America.