Gail Anderson, Lansdale, PA gailanderson@cpm.org
In July of 2017, I had the opportunity to teach at some schools in Narok County, Kenya. My 17-year old daughter and I joined a team of Americans visiting schools built in very rural areas by The Kilgoris Project (www.kilgoris.org). Our goal was to learn about the culture and the school’s project, and to serve as guest teachers in a place where until just a few years ago, children still thought white people were ghosts.
All team members were asked to teach several classes, ranging from preschool through eighth grade. What to teach was up to us to decide: lessons ranged from personal hygiene to Bible stories to solar energy. The purpose in having us teach was to expose the children, as well as the Kenyan teachers, to “something new.” In an area where most people still have to walk to a well for their water every day and often live with no electricity, new teaching ideas typically available on the World Wide Web are virtually non-existent so the goal was exposure to subjects not specifically listed in the Kenyan textbooks.
Of course, being a math teacher and CPM Teacher Leader, I chose to teach a math lesson. The American woman who coordinates the curriculum for The Kilgoris Project’s schools advised me that “Anything that will help them move away from lecture-based teaching where the kids are totally passive” would be helpful, and they would love something to help the students build on what they know, rather than just repeating what they have memorized. As far as background for the class, I knew that there would be 30-40 students in a class, and that they can understand my English if I speak slowly and clearly. I queried further into the content area, and was told that the Class 7 is “working on ratios,” and that Class 8 is “working on construction: they are using geometric shapes and patterns to construct shapes.”
Having taught CPM for over a decade, I have experienced first-hand the benefits of collaborative learning, problem-based teaching and mixed, spaced practice, and I have at my disposal a wide assortment of engaging lessons from which to choose. The only constraint was that I would be able to use only the materials I could carry with me in my suitcase, including the basics such as pencils and paper.
At the first primary school we visited, I was assigned a 6th grade class of about 25 students. I decided to try out Lesson 1.1.4 from Core Connections, Course 2: How Tall is a Million Pennies? For my readers not familiar with Core Connections, Course 2, this lesson has students guess how tall a stack of a million pennies would be, then use some pennies and a ruler to gather data and use a table to calculate the height of a million pennies. (About seven pennies stack to make a centimeter.)

I thought this would be a good lesson to leave with the teachers, as it could be adapted to use readily-available bottle caps (soda here comes in glass bottles, and the bottle caps are easy to collect) instead of money. As I was a visitor, though, I made the lesson more interesting for the kids by bringing a bag of American pennies to use and leave with them. I printed 6-centimeter rulers on cardstock for the students to use, and also some pictures of tall things the kids would be familiar with: a giraffe (they roam the countryside here), the building going up in Nairobi which is planned to be the tallest in Africa, and Mount Kenya.
The students enjoyed learning about American currency and were eager to vote on how tall they thought the pile would be. They did not recognize the mountain when I showed them the photo, but when I said its name, the teacher prompted them and many students recited its height, down to the meter. I had the children cluster into groups of four at their wooden desks. There was quite an age range in the room (many children start school later than five years old, depending on their family situations.) As I passed out the pennies, the younger ones giggled and played with the pennies until I walked near them (sound familiar?) A table of four older girls quickly arrived at a close answer by judging that a stack of ten pennies is 1.5 centimeters tall, and then multiplying by a million.
It was at this point, pretty soon after I had asked the students to work together with their teams, that I glanced over at the classroom teacher, and heard him telling a group “remember, cross-multiply: take this number here and…” He was pretty clearly telling them exactly what they should do, step by step. By the time he got around the room, the chance for exploration was gone and all the students had to do was dutifully complete that division problem by hand (no calculators here, which I think may be a nice way to do the lesson anyway – no senseless pounding of calculator keys. You really need to think about what to do first because if you know it is going to take a long time to do the calculations, you will not want to have to do it twice!)
Rather discouraged by the takeover of rote in my first Kenyan classroom, I decided to use a different lesson for the 7th and 8th grade classes at the next school: a lesson which did not have an answer the teacher would be familiar with. Since I had been told the 8th grade was working with basic shapes, and I had seen formulas for area of quadrilaterals on the board in one of the classrooms, I decided to use an adaptation of Lessons 1.3.1 and 8.1.5 from Core Connections Geometry (CCG). The CCG Chapter 1 lesson uses a puzzle built from various polygons, a foundation for the later lesson which has students find the area of a hexagon (and other composite shapes) by breaking it into pieces. Rather than cutting out many small irregular polygons, I used tangrams, so I could quickly cut all seven pieces out of a square of foamboard. My lesson objective was to explore finding area of complex shapes by breaking them into smaller pieces.
Before handing out the tangrams, I used the first ice-breaker from the Core Connections Alegbra 2 book: Building With Yarn, and we talked about 2- and 3-dimensional shapes. In this problem, students are given an 8-foot long loop of yarn and asked to form various shapes with it. Once one team succeeded at creating a shape, the excitement spread through the room and the students were very actively engaged, helping each other, and showing off what their team created. Even the teacher joined in in the fun. This activity was highly successful for accomplishing the objective of getting the kids to work together.
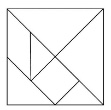

I then explained how I made the tangrams, and drew the above diagram on the board, showing where I made the cuts at various midpoints. My goal was to get them thinking of the sum of the area of the pieces as the area of the entire square. First, they needed to reconstruct the original square from the bag of cut pieces I gave each group. This turned out to be a very challenging task for these kids who did not grow up doing puzzles, and many of them resorted to studying the picture on the board and using that to recreate the square.
Once a group put the square together, I challenged them to find the area of the entire original square, given that the area of one of the small right triangles is one square unit. When I had introduced the lesson, I had asked the students to “turn and tell your neighbor the formula for the area of a
square,” and then almost jumped when the entire of group of students all answered in near-perfect unison: “The area of a square is the square of the side.” They did that for areas of other quadrilaterals and triangles as well. Now, as I circulated among the teams who had successfully pieced together the square, I again experienced that quick response as an answer to my question “If the area of this small triangle is 1, can you figure out what the area of this square is?” Every student’s initial response was to look up at me proudly and recite: “The area of a square is the square of the side!” It took quite a bit of convincing to get them to let go of those formulas for a moment, and consider that the small square was simply twice the small triangle, so they could determine its area without the formula.
I had wanted to give the students time to use the pieces on tangram puzzles, such as problem 1-110 in CCG, but we had already run quite a bit past the “wrap it up warning” given by a teacher assigned to go room to room to let us know what time it was. I looked out the window and saw many students out in the field eating lunch already (their “cafeteria,” rain or shine, is a beautiful hillside with an incredible view of the rolling hills of the countryside!) I invited a couple of students to share their work and then wrapped up with some time for questions. I left the rest of the puzzles and my teacher notes for the teachers, in hopes that they will have interest in trying them out with the students in their next term. This was the end of the middle three-month term for Kenyan students; they have the month of August as term break, and then will finish out their school year with the September-November term.
The thing I probably appreciated the most about the Kenyan schools was their attitude toward the clock… ignore it! Although everyone saw the person come to my room and tell me that I could wrap up the lesson, no one complained – not a student fidgeted – when we kept going for quite some time longer than the rest of the school. The physical circumstances in the Kenyan classrooms I visited were vastly different from what I am accustomed to: there were larger classes, smaller classrooms, smaller desks, benches instead of chairs, no supplies, no backpacks, no computers, no teacher desks, no cell phones, no projector, no clock, no bells, no restrooms (outhouses instead – I will bet kids do not ask for unnecessary trips to the bathroom here!), not even a lightswitch. However, the children themselves are not so different. As my father once told me, “People are people, wherever you go.” Some of the kids were eager to learn, some were eager to play; some wanted to hide in the background, others wanted front stage. As with my American students, the students in Kenya responded very positively to the opportunity to do hands-on, problem-based learning. It was exciting to see CPM’s solid principles working 7,300 miles from home. This reaffirmed yet again my confidence in the strength of our math program as bringing More Math for More People.

