These high-quality high school courses will prepare students with the mathematical problem-solving skills needed for college and for engaging with the world’s problems!
Includes core high school courses
PLUS 4th-Year courses, supporting students interested in advanced placement.

The team also provides a safe space for students to take risks.


Core ideas are synthesized in “Math Notes” boxes purposefully placed sometime after the initial introduction of a concept. This allows students time to explore and build their conceptual understanding of an idea before they are presented with a formal definition, algorithm, or summary of that mathematical concept.
Checkpoints indicate to students where fluency with a skill should occur. Each checkpoint problem has the topic clearly labeled and provides the solution so students can self-assess their progress. Checkpoints also offer examples with detailed explanations and more practice problems with answers included.
CPM provides materials specifically designed to help families support students outside the classroom. Within your student’s digital version of Core Connections, download a complimentary copy of the parent guide. Alternatively, purchase the print version at shop.cpm.org.
The Parent Guide includes:

Teachers will have access to a series of Mathcasts to aid them in preparing lessons. Each Mathcast will outline the problems for that lesson and offer suggestions for facilitating teams.
Chapter 1
1.1 Numbers and Data
1.2 Shapes and Area
1.3 Expressions
Chapter 2
2.1 Ratio Language
2.2 Equivalent Ratios
2.3 Measurement
Chapter 3
3.1 Measures of Center
3.2 Integers
3.3 Absolute Value
3.4 Coordinate Plane
Chapter 4
4.1 Fractions, Decimals, and Percents
4.2 Percents
4.3 Unit Rates in Tables and Graphs
Chapter 5
5.1 Variation in Data
5.2 Area
Chapter 6
6.1 Rules of Operations
6.2 Multiples and Factors
Chapter 7
7.1 Whole Number and Decimal Division
7.2 Fraction Division
Chapter 8
8.1. Algebra Tiles
8.2 Expressions
8.3 Equations and Inequalities
Chapter 9
9.1 Equations and Inequalities Continued
9.2 Rate Problems
Chapter 10
10.1 Two Dimensions
10.2 Three Dimensions
Chapter 11
Chapter 1: Functions
Section 1.1 – Patterns
Section 1.2 – Functions
Chapter 2: Linear Relationships
Section 2.1 – Slope
Section 2.2 – Rate of Change
Section 2.3 – Linear Functions
Chapter 3: Simplifying and Solving
Section 3.1 – Exponential Expressions
Section 3.2 – Multiplying Binomials
Section 3.3 – Equation Solving
Chapter 4: Systems of Equations
Section 4.1 – Writing Equations
Section 4.2 – Solving Systems
Section 4.3 – System Word Problems
Chapter 5: Sequences
Section 5.1 – Exponential Growth
Section 5.2 – Arithmetic Sequences
Section 5.3 – Sequences and Functions
Chapter 6: Modeling Two-Variable Data
Section 6.1 – Line of Best Fit
Section 6.2 – Correlation
Chapter 7: Exponential Functions
Section 7.1 – Exponential Functions
Section 7.2 – Curve Fitting
Chapter 8: Quadratic Functions
Section 8.1 – Factoring
Section 8.2 – Quadratic Representation
Chapter 9: Solving Quadratics and Inequalities
Section 9.1 – Solving Quadratic Equations
Section 9.2 – Linear Inequalities
Section 9.3 – Two-Variable Inequalities
Section 9.4 – Systems of Inequalities
Chapter 10: Solving Complex Equations
Section 10.1 – Two-Way Table Associations
Section 10.2 – Solving Equations
Section 10.3 – Complex Systems
Chapter 11: Functions and Data
Section 11.1 – Transforming Functions
Section 11.2 – Comparing Data
Section 11.3 – Complex Functions
Appendix A: Representing Expressions
Section A.1 – Algebra Tiles and Expressions
Chapter 1: Shapes and Transformations
Section 1.1 – Patterns
Section 1.2 – Rigid Transformations
Section 1.3 – Shapes
Chapter 2: Angles and Measurement
Section 2.1 – Angle Relationships
Section 2.2 – Area
Section 2.3 – Pythagorean Theorem
Chapter 3: Justification and Similarity
Section 3.1 – Similarity
Section 3.2 – Triangle Similarity
Chapter 4: Trigonometry and Probability
Section 4.1 – Tangent Ratio
Section 4.2 – Probability Models
Chapter 5: Completing the Triangle Toolkit
Section 5.1 – Sine and Cosine Ratios
Section 5.2 – Special Right Triangles
Section 5.3 – Law of Sines and Cosines
Chapter 6: Congruent Triangles
Section 6.1 – Congruent Triangles
Section 6.2 – Modeling
Chapter 7: Proof and Quadrilaterals
Section 7.1 – Circle Properties
Section 7.2 – Proofs
Section 7.3 – Coordinate Geometry
Chapter 8: Polygons and Circles
Section 8.1 – Polygon Angles
Section 8.2 – Similarity Ratios
Section 8.3 – Circles
Chapter 9: Solids and Constructions
Section 9.1 – Surface Area and Volumes
Section 9.2 – Geometric Constructions
Chapter 10: Circles and Conditional Probability
Section 10.1 – Circle Properties
Section 10.2 – Two-Way Tables
Section 10.3 – Counting Principles
Chapter 11: Solids and Circles
Section 11.1 – Pyramids and Cones
Section 11.2 – Tangents and Arcs
Chapter 12: Conics and Closure
Section 12.1 – Circle Equations
Section 12.2 – Additional Geometric Topics
Chapter 1: Investigations and Functions
Section 1.1 – Function Properties
Section 1.2 – Function Investigations
Chapter 2: Transformations of Parent Graphs
Section 2.1 – Modeling Functions
Section 2.2 – Transforming Functions
Chapter 3: Equivalent Forms
Section 3.1 – Equivalent Expressions
Section 3.2 – Rational Expressions
Chapter 4: Solving and Intersections
Section 4.1 – Solving Systems
Section 4.2 – Solving Inequalities
Chapter 5: Inverses and Logarithms
Section 5.1 – Inverses
Section 5.2 – Logarithms
Chapter 6 3-D Graphing and Logarithms
Section 6.1 – Three-Dimensional Modeling
Section 6.2 – Logarithms
Chapter 7: Trigonometric Functions
Section 7.1 – Cyclic Models
Section 7.2 – Cyclic Functions
Chapter 8: Polynomials
Section 8.1 – Polynomial Graphs
Section 8.2 – Complex Numbers
Section 8.3 – Polynomial Division
Chapter 9: Randomization and Normal Distributions
Section 9.1 – Sampling
Section 9.2 – Experiments
Section 9.3 – Normal Distributions
Chapter 10: Series
Section 10.1 – Arithmetic Series
Section 10.2 – Geometric Series
Section 10.3 – Binomial Theorem
Chapter 11: Simulating Sampling Variability
Section 11.1 – Probability Simulations
Section 11.2 – Statistical Tests
Section 11.3 – Statistic Analysis
Chapter 12: Analytic Trigonometry
Section 12.1 – Solving Trigonometric Equations
Section 12.2 – Trigonometric Identities
Appendix A: Sequences
Section A.1 – Exponential Growth
Section A.2 – Arithmetic Sequences
Section A.3 – Sequences and Functions
Appendix B: Exponential Functions
Section B.1 – Exponential Functions
Section B.2 – Curve Fitting
Appendix C: Comparing Single-Variable Data
Section C.1 – Data Representations
Chapter 1
Chapter 2
Chapter 3
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
8.1. Algebra Tiles
8.2 Expressions
8.3 Equations and Inequalities
Chapter 9
9.1 Equations and Inequalities Continued
9.2 Rate Problems
Chapter 10
10.1 Two Dimensions
10.2 Three Dimensions
Chapter 11
Chapter 1: Functions
Section 1.1 – Patterns
Section 1.2 – Functions
Section 1.3 – Exponents
Chapter 2: Linear Relationships
Section 2.1 – Slope
Section 2.2 – Rate of Change
Section 2.3 – Linear Functions
Chapter 3: Transformations and Solving
Section 3.1 – Rigid Transformations
Section 3.2 – Multiplying Binomials
Section 3.3 – Equation Solving
Chapter 4: Modeling Two-Variable Data
Section 4.1 – Line of Best Fit
Section 4.2 – Correlation
Chapter 5: Sequences
Section 5.1 – Exponential Growth
Section 5.2 – Arithmetic Sequences
Section 5.3 – Sequences and Functions
Chapter 6: Systems of Equations
Section 6.1 – Word Problems
Section 6.2 – System Solving Methods
Section 6.3 – Elimination in System Solving
Section 6.4 – Solving Systems
Chapter 7: Congruence and Coordinate Geometry
Section 7.1 – Triangle Congruence
Section 7.2 – Coordinate Geometry
Chapter 8: Exponential Functions
Section 8.1 – Exponential Functions
Section 8.2 – Curve Fitting
Chapter 9: Inequalities
Section 9.1 – One-Variable Inequalities
Section 9.2 – Two-Variable Inequalities
Section 9.3 – Systems of Inequalities
Chapter 10: Functions and Data
Section 10.1 – Comparing Data
Section 10.2 – Transforming Functions
Chapter 11: Construction and Closure
Section 11.1 – Constructions
Section 11.2 – Word Problems
Appendix A: Solving Equations
Section A.1 – Algebra Tiles
Chapter 1: Exploring Algebraic and Geometric Relationships
Section 1.1 – Polygons
Section 1.2 – Area Models
Section 1.3 – Angle Relationships
Chapter 2: Justification and Similarity
Section 2.1 – Triangle Congruence
Section 2.2 – Dilations
Section 2.3 – Triangle Similarity
Chapter 3: Probability and Trigonometry
Section 3.1 – Probability Models
Section 3.2 – Tangent Ratio
Chapter 4: Factoring and More Trigonometry
Section 4.1 – Factoring Expressions
Section 4.2 – Sine and Cosine Ratios
Chapter 5: Quadratic Functions
Section 5.1 – Quadratic Properties
Section 5.2 – Solving Quadratic Equations
Chapter 6: More Right Triangles
Section 6.1 – Special Right Triangles
Section 6.2 – Modeling
Chapter 7: Proof and Conditional Probability
Section 7.1 – Proofs
Section 7.2 – Conditional Probability
Chapter 8: Polygons and Circles
Section 8.1 – Triangle Centers
Section 8.2 – Polygon Angles
Section 8.3 – Ratios of Similarity
Chapter 9: Modeling with Functions
Section 9.1 – Nonlinear Functions
Section 9.2 – Systems and Inequalities
Section 9.3 – Rate of Change
Section 9.4 – Inverse Functions
Chapter 10: Circles and More
Section 10.1 – Equation of Circle
Section 10.2 – Circle Properties
Chapter 11: Solids
Section 11.1 – Prisms and Cylinders
Section 11.2 – Surface Area and Volumes
Chapter 12: Counting and Closure
Section 12.1 – Counting Principles
Section 12.2 – Additional Geometric Topics
Chapter 1: Investigations and Functions
Section 1.1 – Function Properties
Section 1.2 – Function Investigations
Chapter 2: Transformations of Parent Graphs
Section 2.1 – Modeling Functions
Section 2.2 – Transforming Functions
Section 2.3 – Completing the Square
Chapter 3: Solving and Inequalities
Section 3.1 – Solving Systems
Section 3.2 – Solving Inequalities
Chapter 4: Normal Distributions and Geometric Modeling
Section 4.1 – Sampling
Section 4.2 – Experiments
Section 4.3 – Normal Distributions
Section 4.4 – Solids
Chapter 5: Inverses and Logarithms
Section 5.1 – Inverses
Section 5.2 – Logarithms
Chapter 6: Simulating Sampling Variability
Section 6.1 – Probability Simulations
Section 6.2 – Statistical Tests
Chapter 7: Logarithms and Triangles
Section 7.1 – Logarithms
Section 7.2 – Law of Sines and Cosines
Chapter 8: Polynomials
Section 8.1 – Polynomial Graphs
Section 8.2 – Complex Numbers
Section 8.3 – Polynomial Division
Chapter 9: Trigonometric Functions
Section 9.1 – Periodic Modeling
Section 9.2 – Transformations
Chapter 10: Series
Section 10.1 – Arithmetic Series
Section 10.2 – Geometric Series
Section 10.3 – Binomial Theorem
Chapter 11: Rational Expressions and Three-Variable Systems
Section 11.1 – Rational Expressions
Section 11.2 – Three Dimensional Modeling
Chapter 12: Analytic Trigonometry
Section 12.1 – Solving Trigonometric Equations
Section 12.2 – Trigonometric Identities

These college preparatory courses, with content for students interested in advanced placement, provide student-centered classroom experiences with problem-based lessons, tools, and routines to engage students with advanced concepts in mathematics.
*Advanced Placement® or AP® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
Chapter 1
1.1 Numbers and Data
1.2 Shapes and Area
1.3 Expressions
Chapter 2
2.1 Ratio Language
2.2 Equivalent Ratios
2.3 Measurement
Chapter 3
3.1 Measures of Center
3.2 Integers
3.3 Absolute Value
3.4 Coordinate Plane
Chapter 4
4.1 Fractions, Decimals, and Percents
4.2 Percents
4.3 Unit Rates in Tables and Graphs
Chapter 5
5.1 Variation in Data
5.2 Area
Chapter 6
6.1 Rules of Operations
6.2 Multiples and Factors
Chapter 7
7.1 Whole Number and Decimal Division
7.2 Fraction Division
Chapter 8
8.1. Algebra Tiles
8.2 Expressions
8.3 Equations and Inequalities
Chapter 9
9.1 Equations and Inequalities Continued
9.2 Rate Problems
Chapter 10
10.1 Two Dimensions
10.2 Three Dimensions
Chapter 11
Chapter 1: Preparing for Your Journey
Section 1.1 – Modeling with Functions
Section 1.2 – Additional Functions
Section 1.3 – Radian Measure
Chapter 2: Functions and Trigonometry
Section 2.1 – Function Properties
Section 2.2 – Sine and Cosine Graphs
Section 2.3 – Trigonometric Equations
Chapter 3: Algebra and Area Under a Curve
Section 3.1 – Equations and Expressions
Section 3.2 – Area Under a Curve
Chapter 4: Polynomial and Rational Functions
Section 4.1 – Polynomial Functions
Section 4.2 – Rational and Reciprocal Functions
Section 4.3 – Inequalities and Applications
Chapter 5: Exponentials and Logarithms
Section 5.1 – Exponentials
Section 5.2 – Logarithms
Chapter 6: Triangles and Vectors
Section 6.1 – Law of Sines and Cosines
Section 6.2 – Vectors
Chapter 7: Limits and Rates
Section 7.1 – Limits Introduction
Section 7.2 – Rates of Change
Chapter 8: Extending Periodic Functions
Section 8.1 – Periodic Function Modeling
Section 8.2 – Reciprocal Trigonometric Functions
Section 8.3 – Trigonometric Identities
Chapter 9: Matrices
Section 9.1 – Matrices
Section 9.2 – Linear Transformations
Chapter 10: Conics and Parametric Functions
Section 10.1 – Conic Sections
Section 10. 2 – Parametrica Functions
Chapter 11: Polar Functions and Complex Numbers
Section 11.1 – Polar Functions
Section 11.2 – Complex Numbers
Chapter 12: Series and Statistics
Section 12.1 – Series
Section 12.2 – Binomial Theorem
Section 12.3 – Expected Value
Chapter 13: Precalculus Finale
Section 13.1 – Limits
Section 13.2 – Area Under Curve
Section 13.3 – Definition of Derivative
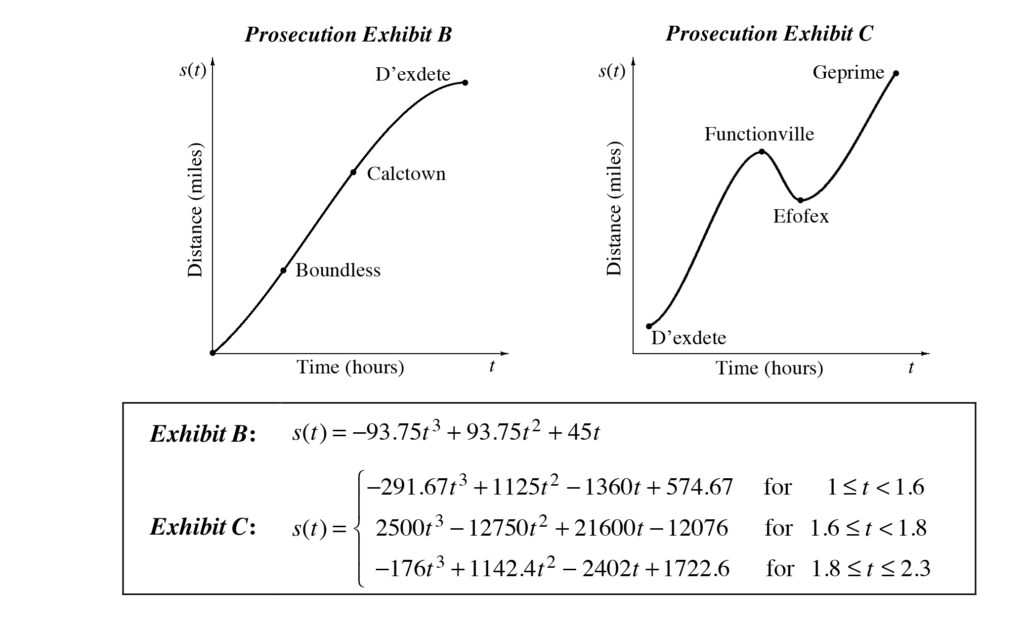
2.3.4
Defining Concavity
4.4.1
Characteristics of Polynomial Functions
5.2.6
Semi-Log Plots
5 Closure
Closure How Can I Apply It? Activity 3
9.3.1
Transition States
9.3.2
Future and Past States
10.3.1
The Parametrization of Functions, Conics, and Their Inverses
10.3.2
Vector-Valued Functions
11.1.5
Rate of Change of Polar Functions
Chapter 1
Chapter 2
Chapter 3
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
8.1. Algebra Tiles
8.2 Expressions
8.3 Equations and Inequalities
Chapter 9
9.1 Equations and Inequalities Continued
9.2 Rate Problems
Chapter 10
10.1 Two Dimensions
10.2 Three Dimensions
Chapter 11
Chapter 1: A Beginning Look at Calculus
Section 1.1 – Applying Rates and Distance
Section 1.2 – Properties of Functions
Section 1.3 – Finite Differences
Section 1.4 – Distance and Velocity
Section 1.5 – Area and Slope
Chapter 2: Rates, Sums, Limits, and Continuity
Section 2.1 – Area Under a Curve –
Section 2.2 – Limits and Continuity
Section 2.3 – Local Linearity
Section 2.4 – Improving Approximation
Chapter 3: Slope and Curve Analysis
Section 3.1 – The Power Rule
Section 3.2 – Derivatives
Section 3.3 – Differentiability
Chapter 4: The Fundamental Theorem of Calculus
Section 4.1 – Definite Integrals
Section 4.2 – The Fundamental Theorem of Calculus
Section 4.3 – Instantaneous Velocity
Section 4.4 – Area Between Curves
Section 4.5 – Newton’s Method
Chapter 5: Derivative Tools and Applications
Section 5.1 – Distance, Velocity, and Acceleration Functions
Section 5.2 – Derivative Rules
Section 5.3 – Optimization Problems
Section 5.4 – Chain Rule Extension
Section 5.5 – Limits of Indeterminate Forms
Chapter 6: More Tools and Theorems
Section 6.1 – Derivatives of Exponential Functions
Section 6.2 – Implicit Differentiation
Section 6.3 – Derivatives of Inverse Functions
Section 6.4 – Mean Value Theorem
Section 6.5 – Improper Integrals
Chapter 7: Related Rates and Integration Tools
Section 7.1 – Related Rates Applications
Section 7.2 – Integration with u-Substitution
Section 7.3 – Differential Equations Applications
Section 7.4 – Integration By Parts
Chapter 8: Volume
Section 8.1 – Disk and Washer Problems
Section 8.2 – Volume Calculation Methods
Section 8.3 – Cross-Section Problems
Section 8.4 – Arc Length
Chapter 9: Pre-Calculus Review
Section 9.1 – Geometric Series
Section 9.2 – Parametric Equations
Section 9.3 – Vectors
Section 9.4 – Polar Equations
Chapter 10: Convergence of Series
Section 10.1 – Convergence Tests
Section 10.2 – More Logistic Differential Equations
Section 10. 3 – Polynomials to Approximate Curves
Section 10.4 – Absolute Convergence
Chapter 11: Polar and Parametric Functions
Section 11.1 – Area Bounded by a Polar Curve
Section 11.2 – Applied Calculus in Component Form
Section 11.3 – Slopes of Polar Curves
Section 11.4 – Parametric Functions Application
Chapter 12: Approximating Functions and Error
Section 12.1 – Taylor Polynomials
Section 12.2 – Intervals of Convergence
Section 12.3 – Error Bound
Section 12.4 – Indeterminate Forms
Chapter 1: Representing Data
Section 1.1 – Histograms and Stem
Section 1.2 – Choosing Appropriate Statistics
Section 1.3 – Percentiles
Chapter 2: Two-Variable Quantitative Data
Section 2.1 – Scatterplots and Association
Section 2.2 – Correlation
Chapter 3: Multivariable Categorical Data
Section 3.1 – Probability and Two-Way Frequency Tables
Section 3.2 – Problem Solving with Categorical Data
Chapter 4: Studies and Experiments
Section 4.1 – Survey Design
Section 4.2 – Experiments
Chapter 5: Density Functions and Normal Distributions
Section 5.1 – Density Functions
Section 5.2 – The Standard Normal Distribution
Chapter 6: Discrete Probability Distributions
Section 6.1 – Discrete Random Variable
Section 6.2 -Binomial Distribution
Section 6.3 – Geometric Distribution
Chapter 7: Variability in Categorical Data Sampling
Section 7.1 – Sampling Distributions
Section 7.2 – Confidence Intervals
Chapter 8: Drawing Conclusions From Categorical Data
Section 8.1 – Introduction to Hypothesis Testing
Section 8.2 – Types of Errors and Power
Section 8.3 – Two-Sample Proportion Hypothesis Tests
Chapter 9: Chi-Squared Inference Procedures
Section 9.1 – Chi-Squared Goodness of Fit
Section 9.2 – Chi-Squared Tests
Chapter 10: Drawing Conclusions From Quantitative Data
Section 10.1 – Sampling Distributions
Section 10.2 – The Central Limit Theorem
Section 10.3 – t-Distribution
Chapter 11: Comparing Means and Identifying Tests
Section 11.1 – Tests for the Difference of Two Means
Section 11.2 – Identifying and Implementing an Appropriate Test
Chapter 12: Inference for Regression
Section 12.1 – Inference for the Slope of the Regression Line
Section 12.2 – Linearity
Chapter 13: ANOVA and Beyond!
Section 13.1 – Chi-Squared and F-Distribution
Section 13.2 – One-Way ANOVA
Section 13.3 – Sign and Mood’s Median Tests

2.3.4
Defining Concavity
4.4.1
Characteristics of Polynomial Functions
5.2.6
Semi-Log Plots
5 Closure
Closure How Can I Apply It? Activity 3
9.3.1
Transition States
9.3.2
Future and Past States
10.3.1
The Parametrization of Functions, Conics, and Their Inverses
10.3.2
Vector-Valued Functions
11.1.5
Rate of Change of Polar Functions

This professional learning is designed for teachers as they begin their implementation of CPM. This series contains multiple components and is grounded in multiple active experiences delivered over the first year. This learning experience will encourage teachers to adjust their instructional practices, expand their content knowledge, and challenge their beliefs about teaching and learning. Teachers and leaders will gain first-hand experience with CPM with emphasis on what they will be teaching. Throughout this series educators will experience the mathematics, consider instructional practices, and learn about the classroom environment necessary for a successful implementation of CPM curriculum resources.
Page 2 of the Professional Learning Progression (PDF) describes all of the components of this learning event and the additional support available. Teachers new to a course, but have previously attended Foundations for Implementation, can choose to engage in the course Content Modules in the Professional Learning Portal rather than attending the entire series of learning events again.
The Building on Instructional Practice Series consists of three different events – Building on Discourse, Building on Assessment, Building on Equity – that are designed for teachers with a minimum of one year of experience teaching with CPM instructional materials and who have completed the Foundations for Implementation Series.
In Building on Equity, participants will learn how to include equitable practices in their classroom and support traditionally underserved students in becoming leaders of their own learning. Essential questions include: How do I shift dependent learners into independent learners? How does my own math identity and cultural background impact my classroom? The focus of day one is equitable classroom culture. Participants will reflect on how their math identity and mindsets impact student learning. They will begin working on a plan for Chapter 1 that creates an equitable classroom culture. The focus of day two and three is implementing equitable tasks. Participants will develop their use of the 5 Practices for Orchestrating Meaningful Mathematical Discussions and curate strategies for supporting all students in becoming leaders of their own learning. Participants will use an equity lens to reflect on and revise their Chapter 1 lesson plans.
In Building on Assessment, participants will apply assessment research and develop methods to provide feedback to students and inform equitable assessment decisions. On day one, participants will align assessment practices with learning progressions and the principle of mastery over time as well as write assessment items. During day two, participants will develop rubrics, explore alternate types of assessment, and plan for implementation that supports student ownership. On the third day, participants will develop strategies to monitor progress and provide evidence of proficiency with identified mathematics content and practices. Participants will develop assessment action plans that will encourage continued collaboration within their learning community.
In Building on Discourse, participants will improve their ability to facilitate meaningful mathematical discourse. This learning experience will encourage participants to adjust their instructional practices in the areas of sharing math authority, developing independent learners, and the creation of equitable classroom environments. Participants will plan for student learning by using teaching practices such as posing purposeful questioning, supporting productive struggle, and facilitating meaningful mathematical discourse. In doing so, participants learn to support students collaboratively engaged with rich tasks with all elements of the Effective Mathematics Teaching Practices incorporated through intentional and reflective planning.