Teaching mathematics to teenagers can be a challenging task. In a single classroom, there are often students who are still struggling to remember their multiplication facts, while other students can solve a complex equation for x. Even more, there are also students who struggle with solving real-world problems when taken out of the context of their math classroom. For example, when working exclusively with the Pythagorean Theorem, many students might be able to solve a word problem after working through basic computation problems on the same subject. Yet, after a few weeks, when given a similar word problem students often forget how to solve the problem without being told which formula or process to use. I have heard many teachers say that students know how to solve math problems in the computational form, but struggle with knowing what the question is asking and which math topic to use to solve the problem.
Many teachers try to find strategies to help students solve real-world problems. Teachers might say that “of ” means you multiply or “total” means you add. They might say that “per” and “every” tells us about the unit rate. Most of these strategies, however, are procedural and do not encourage students to understand the problem or to think about different ways to solve it. Using similar vocabulary and strategies across all content areas can help students understand how to solve math word problems.
Metacognition is the conscious awareness of one’s thinking. English and reading teachers across all grade levels explicitly teach metacognition strategies to students to help them read complex texts. They teach students to think about their reading first purposefully and then automatically. These metacognitive strategies give readers control over their learning process. There are two metacognitive strategies that language arts teachers use that can be implemented in a mathematics classroom: visualizing and inferencing.
We often associate visualizing in a math classroom with students and teachers drawing pictures or diagrams. However, as Jennifer Piggott and Liz Woodham state, “Visualizing has a much wider role to play in problem-solving including supporting the development of ideas and facilitating communication of results and understanding.” (Piggott & Woodham, 2009) To help students understand how to solve a real-world problem, focus the visualizations so that they support the development of the ideas of how to approach the problem. Piggott and Woodham have identified three purposes for visualizing:
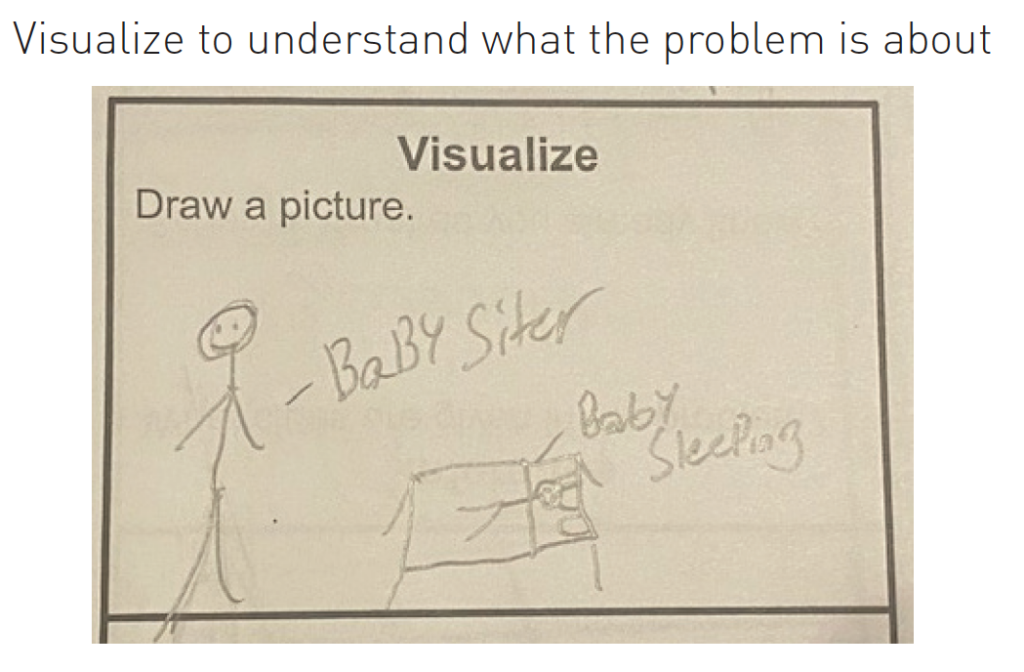
1. Visualize to understand what the problem is about.
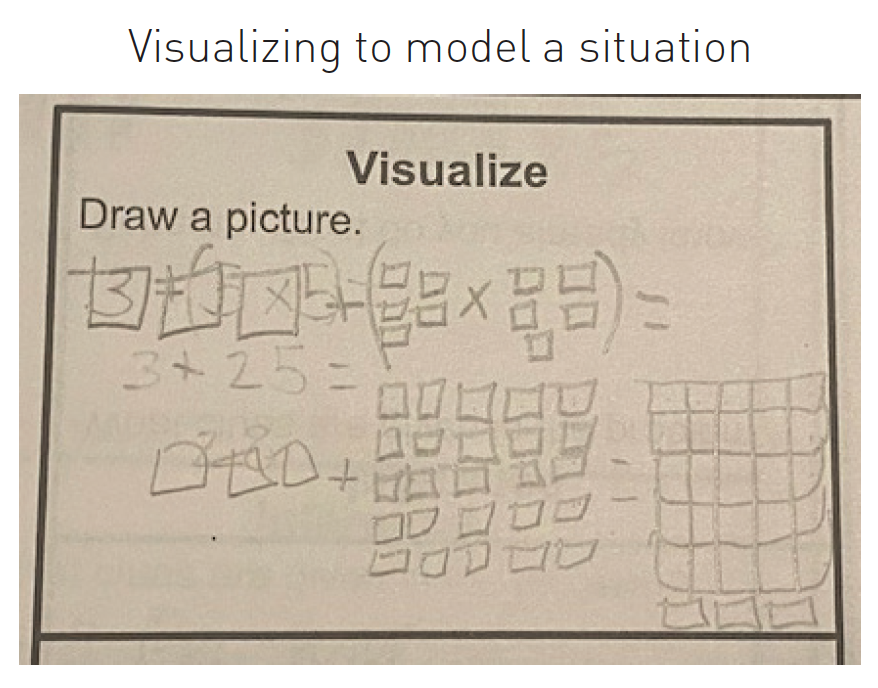
2. Visualize to model a situation.
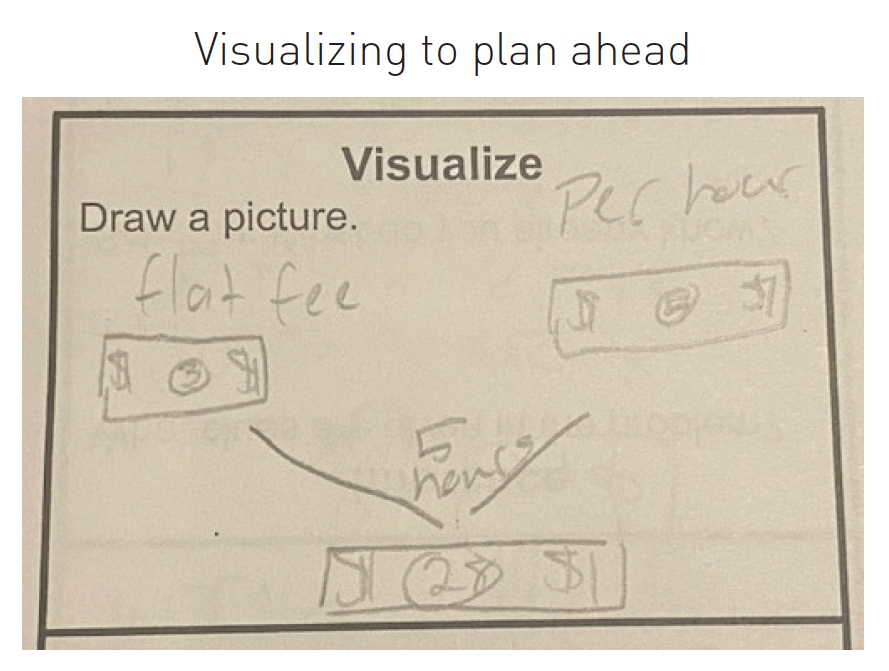
3. Visualize to plan ahead.
The figure shows an example of these three different purposes of visualizations in a math classroom. The students in this class are all drawing pictures and models in order to understand the context of the problem, yet they visualize it in different ways.
Question: For babysitting, Nicole charges a flat fee of $3, plus $5 per hour. How much money will she make if she baby-sits 5 hours?
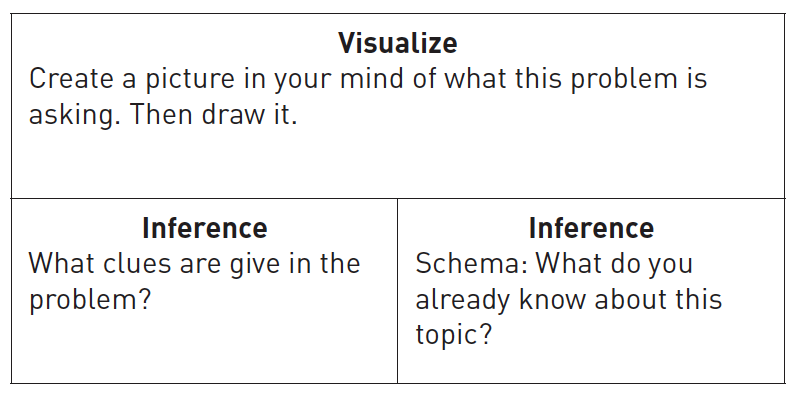
The second metacognitive strategy reading teachers use that mathematics teachers can implement in their problem-solving lessons is teaching students to make inferences. Inferences in a reading classroom include having students use clues from the text and their own thinking to make predictions. Students can use two prompts in their math class in order to make an inference about their word problem:
1. What clues are given in the problem?
2. What do I already know about this topic?
The figure shows how a student answered these two questions and developed an inference about their current math problem. In the example, the student wrote what clues were given in the problem. This is another way students can annotate a text. The goal is for students to begin thinking about what the problem is giving them before they immediately try answering it. The second question has them begin thinking about ways to solve the problem. They are not asked to solve it yet but are instead asked to list all the ways they could potentially solve the problem.
Question: You have a square blanket that has an area of 25 square inches. What is the length of 1 side of the blanket?

In this example, the student writes that they know the area of the blanket is 25 square inches (What clues are given in the problem?) and that they know that area is figured out through multiplication (What do I already know about this topic?). Using these two questions, they are now able to work towards solving the problem. Teachers can help create a class list of the different math topics associated with the problem using each of the student’s answers to the second question. This encourages autonomy in how students can solve open-ended problems and shares different connections that some students may not have considered.
Having students use both metacognitive strategies together can better prepare them for solving real-world problems. Using the template, students have a process for problem-solving that does not turn the problems into procedural problems or rely on tricks. Using the strategies of visualizing and inferencing together better equips students with a thinking process that allows them to understand the problem and the math skills needed to solve each real-world problem.
References
Schema theory. (n.d.). Retrieved from http://bb.plsweb.com/FLBR/m5/m5a_key0.html
Kenney, J. M. (2005). Literacy strategies for improving mathematics instruction. Association for Supervision and Curriculum Development.
Piggott, J., & Woodham, L. (2009). Thinking through, and by, visualising. NRICH. Retrieved from https://nrich.maths.org/6447

Keri Whitaker
Louisville, KY, keri.whitaker@jefferson.kyschools.us

