These high quality middle school math programs prepare students with powerful mathematical thinking and problem solving skills.
Includes two unique middle school programs and a support class
Middle School Math Curriculum that Centers Student Problem Solving
• Meaningful Mathematics
• Multimodal program utilizing both digital & print materials
• Dynamic teacher-guided pacing technology
• Intentional mix of digital, print, and manipulatives
• Consumable student book called the Mathematician’s Notebook
• CPM’s time-tested program
• Based on research & CPM’s Three Pillars
• Option of digital and/or print materials
• English and Spanish
What does a full blend of print and digital look like? In this multimodal series, digital and print materials work in tandem to maximize student engagement. The choice of medium for each aspect of a lesson is based on how and where students learn best.
A personal notebook where students record the messy work of learning as they highlight key concepts, questions, rough draft thinking, mistakes, corrections, and their inspirations. Diagrams and graphs are included for students to work with, and plenty of space is provided to give students room for error and experimentation.
Concise goals for each lesson are presented to the teacher and to students in the chapter introductions, referenced in the Reflection & Practice problems, and revisited in Chapter Closures. The Mathematician’s Notebook contains a printed copy of the Learning Targets where students can keep track of their progress throughout the course.
Problems are designed to facilitate student learning per the learning intent. To maximize student sensemaking and engagement, lessons have been intentionally constructed using a variety of Venues for student work, such as vertical non-permanent surfaces, external links, embedded technology-enhanced activities, and the Mathematician’s Notebook.
Here are examples of different venues:
Inspiring Connections guides teachers through lessons.
The authors describe how they envision the lesson progressing. These notes are summarized into brief descriptions, which can serve as a reminder after reading the full Authors’ Vision.
The Lesson at a Glance provides a quick orientation to the lesson. It lists things to consider as you begin to prepare to teach the lesson: the overview, learning intent, materials needed for the lesson, aligning standards, and additional resources.
Lessons are designed for students to work in teams during a 45-minute period.
Students collaborate in teams for the large majority of class time. As a means to help all students have a voice and be an integral part of their team, four roles are presented in the Prelude and referred to throughout the curriculum. The roles are Representative, Coordinator, Organizer, and Investigator.
A variety of Study Team and Teaching Strategies (STTS) are suggested in the Authors’ Vision throughout Inspiring Connections. These strategies may be used to help structure team interactions and facilitate engagement. As you gain experience with the curriculum and your students, you will likely develop your own favorite strategies to use regularly.
Inspirations & Ideas is a compilation of lessons, arranged appropriately in units, that convey multiple objectives. Although each unit may not fully address a single objective, as a compilation the objectives are met. The course does not attempt to address every content standard in the 8th grade curriculum. Rather the math content in the course is used as a vehicle to change students’ beliefs and attitudes about math. Inspirations & Ideas focuses on the following themes:
Incorrect ideas are often necessary to develop correct ideas. • Honoring mistakes • Trial and error/Guess and Check Mathematics is visual. • Multiple representations • Patterns Effective communication in mathematics should be practiced. • Giving and receiving effective math feedback • Justifying mathematics verbally and in writing Problem solving strategies make problems accessible. • Working backwards • Making the problem smaller • Organize information Building relationships is vital to a positive classroom environment. * Individual progress checks with the teacher • Student reflection journals • Goal setting Students can re-engage with mathematics in new ways. • Ratio • Proportion • Equivalence • Solving • Numeracy • Patterns • Graphing • Fractions • Exponents
© 1989-2023 CPM EDUCATIONAL PROGRAM All rights reserved. CPM Educational Program is a 501(c)(3) educational nonprofit corporation.
0.1.1
Who are my classmates?
0.1.2
How do I work collaboratively?
0.1.3
What questions can I ask?
0.1.4
How can I categorize my words?
0.1.5
How can I communicate my ideas?
0.1.6
How can the team build this together?
0.1.7
What do we need to work togethe
1.1 Numbers and Data
1.1.1 How should data be placed on this line?
1.1.2 Where do these numbers belong on this line?
1.1.3 How can I use two lines to solve problems?
1.1.4 How can data be used to answer a question?
1.1.5 How are histograms helpful?
1.1.6 How else can data be displayed?
1.2 Shapes and Area,
1.2.1 How can I write equivalent expressions in area and perimeter?
1.2.2 What shapes make up the polygon?
1.2.3 How can I make it a rectangle?
1.3 Expressions
1.3.1 How can I describe it using symbols?
1.3.2 What are the parts of an expression?
1.3.3 How do I work with decimals?
1.3.4 How do I multiply multi-digit decimals?
1.3.5 How can I represent the arrangement?
2.1 Ratio Language
2.1.1 How can I compare two quantities?
2.1.2 How can I write ratios?
2.1.3 How can I see ratios in data representations?
2.2 Equivalent Ratios
2.2.1 How can I visualize ratios?
2.2.2 How can I see equivalent ratios in a table?
2.2.3 How can I see equivalent ratios in a double number line?
2.2.4 How can I see equivalent ratios in tape diagrams?
2.2.5 How can I use equivalent ratios?
2.2.6 What do these represent?
2.3 Measurement
2.3.1 What are the measurements?
2.3.2 What are the units?
2.3.3 How can I convert units
3.1 Measures of Center
3.1.1 How can I measure the center?
3.1.2 How else can I measure the center?
3.1.3 Which is the better measure of center?
3.1.4 What happens when I change the data?
3.2 Integers
3.2.1 What numbers do I see?
3.2.2 What number is this?
3.2.3 What does a number line say about a number?
3.2.4 How do I compare different types of numbers?
3.3 Absolute Value
3.3.1 How do I describe the location?
3.3.2 How far do I walk?
3.3.3 Which one is greater?
3.3.4 How do I communicate mathematically?
3.4 Coordinate Plane
3.4.1 How can you precisely indicate a location?
3.4.2 What is the correct order?
3.4.3bWhat symbol represents me?
4.1 Fractions, Decimals, and Percents
4.1.1 How can I tell if the ratios are equal?
4.1.2 What does “percent” mean?
4.1.3 How can I convert a fraction?
4.1.4 How can I convert a percent?
4.1.5 How can I convert a decimal?
5.1 Variation in Data
5.1.1 How do I ask a statistical question?
5.1.2 What does each representation say about the data?
5.1.3 What does the box in a box plot represent?
5.1.4 How else can I describe data?
5.2 Area
5.2.1 What is the height?
5.2.2 Can I reconfigure a parallelogram into a rectangle?
5.2.3 How do I calculate the area?
5.2.4 How many triangles do I need?
5.2.5 What is my perspective?
5.2.6 Is it fair to play by the rules?
5.2.7 What shapes do I see?
5.3 Fractions
5.3.1 How can I represent fraction multiplication?
5.3.2 How can I multiply fractions?
5.3.3 How can I multiply mixed numbers?
6.1 Rules of Operations
6.1.1 What does it mean?
6.1.2 What do mathematicians call this?
6.1.3 How much should I ask for?
6.1.4 How can I write mathematical expressions?
6.1.5 How do mathematicians abbreviate?
6.1.6 In what order should I evaluate?
6.2 Multiples and Factors
6.2.1 When will they be the same?
6.2.2 What are multiples?
6.2.3 What do they have in common?
6.2.4 Who is your secret valentine?
6.2.5 How can I understand products?
6.2.6 How can I rewrite expressions?
6.2.7 Which method do I use?
7.1 Whole Number and Decimal Division
7.1.1 How can I share equally?
7.1.2 Which strategy is the most efficient?
7.1.3 How can I write the number sentence?
7.1.4 How can I divide decimals?
7.1.5 How should the problem be arranged?
7.2 Fraction Division
7.2.1 What if the divisor is a fraction?
7.2.2 How many fit?
7.2.3 How can I visualize this?
7.2.4 What is common about this?
7.2.5 How can I use a Giant One?
7.2.6 Which method is most efficient?
8.1. Algebra Tiles
8.1.1 What do these shapes represent?
8.1.2 What does a group of tiles represent?
8.1.3 What is an equivalent expression?
8.1.4 Which terms can be combined?
8.1.5 What do the numbers mean?
8.1.6 What can a variable represent?
8.2 Expressions
8.2.1 How can I count it?
8.2.2 What if the size of the pool is unknown?
8.2.3 How can I use an algebraic expression?
8.3 Equations and Inequalities
8.3.1 Which values make the equation true?
8.3.2 How can patterns be represented?
8.3.3 What is the equation?
8.3.4 How many could there be?
1.1 Data and Graphs
1.1.1 How can I represent data?
1.1.2 How can I use data to solve a problem?
1.1.3 Is the roller coaster safe?
1.1.4 Is there a relationship?
1.1.5 What is the relationship?
| 8.1 | Introduction to Functions | |
| 8.1.1 | How can you (de)code the message? |
| 8.1.2 | How can a graph tell a story? |
| 8.1.3 | What can you predict? |
| 8.1.4 | Which prediction is best? |
| 8.1.5 | How does the output change based on the input? |
| 8.1.6 | How do you see the relationship? |
8.2 | Characteristics of Functions | |
| 8.2.1 | What is a function? |
| 8.2.2 | How can you describe the relationship? |
| 8.2.3 | How do I sketch it? |
| 8.2.4 | How many relationships are there? |
8.3 | Linear and Nonlinear Functions | |
| 8.3.1 | Is it linear or nonlinear? |
| 8.3.2 | What clues do ordered pairs reveal about a relationship? |
| 8.3.3 | What other functions might you encounter? |
| 9.1 | Volume | |
| 9.1.1 | Given the volume of a cube, how long is the side? |
| 9.1.2 | What if the base is not a polygon? |
| 9.1.3 | What if the layers are not the same? |
| 9.1.4 | What if it is oblique? |
| 9.1.5 | What if it is a three-dimensional circle? |
9.2 | Scientific Notation | |
| 9.2.1 | How can I write very large or very small numbers? |
| 9.2.2 | How do I compare very large numbers? |
| 9.2.3 | How do I multiply and divide numbers written in scientific notation? |
| 9.2.4 | How do I add and subtract numbers written in scientific notation? |
| 9.2.5 | How do I compute it? |
9.3 | Applications of Volume | |
| 9.3.1 | What does a volume function look like? |
| 9.3.2 | What is the biggest cone? |
| 9.3.3 | How do all the items fit together? |
| 10.1 | Explorations and Investigations | |
| 10.1.1 | How close can I get? |
| 10.1.2 | Can you make them all? |
| 10.1.3 | How many triangles will there be? |
| 10.1.4 | What’s my angle? |
| 10.1.5 | Function-function, what’s your function? |
| 10.1.6 | Is it always true? |
| 10.1.7 | What’s right? |
| 10.1.8 | What’s your story? |
LEARNING LOG
Write a Learning Log entry to summarize what you learned today about the Giant One and its uses. Include examples of how the Giant One is used. Title this entry “The Giant One and Equivalent Fractions” and label it with today’s date.
LEARNING LOG
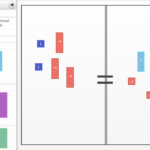
Make a rectangle from any number of tiles. Your rectangle must contain at least one of each of the following tiles: x^2, y^2 , x, y and xy. Sketch your rectangle in your Learning Log and write its area as a product and as a sum. Explain how you know that the product and sum are equivalent. Title this entry “Area as a Product and as a Sum” and label it with today’s date.
PI-10. WAY TO GO!
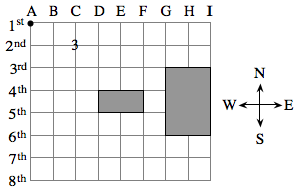
The map at right shows the streets in Old Town. Assume Jacqueline is standing at the corner of A and 1st Streets. Assume Jacqueline will only walk South or East. The shaded rectangles represent large buildings. Assume Jacqueline will not pass through any buildings.
The number “3” at the intersection of C and 2nd Streets means that there are three different ways she can get there from her starting position. What are those three ways? Describe them in words.
How many different ways can she walk to the corner of F and 4th Streets?
How many different ways can she walk to the corner of D and 5th Streets?
Explain how you can use your answers to parts (b) and (c) to find the number of ways she can walk to the corner of F and 5th Streets. Why does this make sense?
Find the number of different ways she can walk to the corner of I and 8th Streets.
How could you change the map so that Jacqueline has only 7 ways to get to the corner of D and 3rd streets? You can remove blocks or add them.
This professional learning is designed for teachers as they begin their implementation of CPM. This series contains multiple components and is grounded in multiple active experiences delivered over the first year. This learning experience will encourage teachers to adjust their instructional practices, expand their content knowledge, and challenge their beliefs about teaching and learning. Teachers and leaders will gain first-hand experience with CPM with emphasis on what they will be teaching. Throughout this series educators will experience the mathematics, consider instructional practices, and learn about the classroom environment necessary for a successful implementation of CPM curriculum resources.
Page 2 of the Professional Learning Progression (PDF) describes all of the components of this learning event and the additional support available. Teachers new to a course, but have previously attended Foundations for Implementation, can choose to engage in the course Content Modules in the Professional Learning Portal rather than attending the entire series of learning events again.
