Michael Parham, Adams-Friendship High School, Adams, WI
In our district, we had the fortunate opportunity to have a CPM math coach help us implement effective strategies with the curriculum. A lot of good discussions have come out of the work with our coach, including how to use teamwork more effectively by revising team roles, the importance of writing common assessments as a math department, but most importantly, how to conduct Number Talks with my classes. Usually Number Talks occur in the elementary grades, but we asked ourselves: Why can’t we use them at the high school level? That is exactly what we wanted to try. So our journey began.
My classes are composed of various levels of students with about 75% being classified as special education or having behavioral issues. Many of my students lacked mathematical fluency and confidence in the classroom. We pondered what we could do about helping them. The plan we came up with was to do a Number Talk on both Tuesdays and Thursdays for at least eight weeks. We knew that this needed to be part of our regular routine and not just a short trial.
We started off with Dot Talks to get everybody used to the process. Dot Talks are about students developing strategies for counting without counting by 1s. For instance, for the picture at right, some students will see this as 4 + 3 + 4 = 11 dots, while others might see this as 2(4) + 3 = 11. Both give the same answer, but with different approaches for counting the dots. We want the students to be able to use a variety of strategies to improve their math fluency. As they become more comfortable with numbers and the different strategies, students will be able to use them to explore deeper concepts during class. There are multiple strategies possible with any Dot or Number Talk, but only one correct answer.

For all of our talks, we came up with a few guidelines:
- You have to justify your answer by explaining your strategy, not just giving an answer.
- Mental math only! You cannot use a calculator or paper/pen.
- You should respect others when they share their ideas, but challenge them if you do not understand or disagree.
- The Number Talks would be limited to no more than ten minutes.
Most Number Talks were just a little bit longer than five minutes. After ten minutes, the amount of engagement was diminished.
After two weeks of Dot Talks, we switched over to Number Talks. We started off with two-digit addition problems because addition is one of the first concepts students learn, and so most students feel comfortable with addition. The process started off very slowly, with only a few students contributing comments. The students that did contribute were using the traditional algorithm in their heads, imaging one number above the other, as they added the columns. Every once in awhile, a student would share a unique strategy, but this was not the norm. I knew there had to be something else I could do to promote more critical thinking about these problems. I wanted the students to enjoy the problems and have an informal conversation about the multiple ways that we can find a solution.
The first breakthrough I had was when I realized that I had to have an open mind. Students were coming up with so many different strategies including some that I did not even see myself. I emphasized that there is only one right answer, but many different ways to get there, and that you can only use “legal moves” in your strategy. During a Number Talk, my role is to write down exactly what the student says. It is not easy to write down an incorrect strategy without making a face, but I had to do it. I know from personal experience, as well as my professional development time learning about fixed versus growth mindset, people learn more from a mistake than they do when they are always getting an answer correct. For example, I would record a student’s strategy, and I would leave it as it was. I would move onto the next student’s strategy. Once several people shared, someone would challenge an earlier strategy, or a student would correct his own strategy.
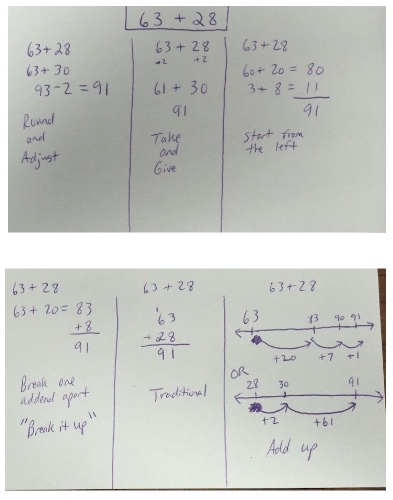
Even after discussing these methods, students till seemed to rely on the traditional algorithm. The second breakthrough I had was to write down the name of the strategy as the students used it. All of a sudden, students started using more of these new strategies. A student said to me, “I think most of us were looking for the weird strategies, instead of the easy ones.”
This might sound great in theory, but how did it actually work in my classroom? We saw a lot of progress. Students were using more strategies on a regular basis, more students were responding to the given problem, and students were displaying more confidence with their explanations. These improvements were not limited to the Number Talks. We saw improvement in student confidence while working on their lesson/homework, while working with their teams, and when I would ask them questions related to bigger concepts covered in the classroom. So where do we go now? When our math coach has moved on, my class will continue to use Number Talks and modify them to connect directly to higher-level concepts that we see in algebra.
On a special note, I could not have done all of this without the help of my math coach Mark Ray. On a weekly basis, I would record my class, share them online using Swivl software, and then he would comment on my videos. The following week we would Skype and talk about how the week went and what changes we could do to make things better. For example, the last change we made was to have everybody share, even if it was a strategy that was already introduced.


