Brian Ryczkowski, Green Bay, WI, bryczkowski@ashwaubenonk12.org
What was I doing before?
No, not before COVID—though I did start this article in March of 2020. What was I doing in the classroom?
I have had the privilege of working with two great CPM coaches: John Hayes and Lorna Vazquez. In 2020, when with Lorna, we decided the coaching goal we would pursue would be: Elicit and use evidence of student thinking. Specifically, the student behavior we wanted to consider was teaching practice 8: Students reveal their mathematical understanding, reasoning, and methods in written work and classroom discourse.
In 2017 and 2021, when working with John Hayes, lesson planning revolved around these questions:
- What is the goal of the lesson?
- Where might students struggle and how can we support them to be productive?
- Where does the lesson hinge?
- When can they get up and move during the lesson?
- What i the closure?
Through all of this work, everything revolves around the goal of the lesson. What is the goal of the lesson? It is what we have all come to know as Learning Targets, I can statements, Success Criteria—the multitudes of the verbiage used to get at the heart of what a lesson truly is.
At the start of every lesson, I have a student volunteer read the lesson opening, as CPM suggests. I use Activinspire, which is similar to SMART Notebook. After the student finishes reading, the next slide is one I have pre-generated, and it states the goal of the lesson. The goal is always written as a question, and I try to make it as short and student-friendly as possible. For example, in Core Connections Algebra, one of our questions recently was, What is y = mx + b? The learning goal comes from Learning Log prompts and the Lesson Objective in the teacher’s edition. Here is what they see.

At Ashwaubenon High School, each student has a Toolkit where they write the answer to the goal of the lesson. Their Toolkit is where they write their Learning Log entries, definitions, examples, and all of the evidence of learning. One of the conversations we have early in the year is that our notebook is our “sloppy copy” and our Toolkit is our “final copy.” Everything that student teams read about and write intheir notebook–problems they complete and conversations they have—are all geared towards answering the goal of the lesson.
I am fortunate enough to have a whiteboard wall in my classroom. When we show students the goal of the lesson at the start of class, I go to the wall and write the question as high on the back wall as I possibly can. While I write the question on the wall, a student volunteer reads the question while everyone else writes the question in their Toolkit. Then, I tell them to hide their Toolkit under their book. We do this to promote the idea of “beginning with the end in mind.” Early in the year, I also say “You will know if you have been successful if you can answer that question at the end of class.”
During the lesson, I try to use several STTS to encourage students to talk and listen to each other. A few that I swear by are Board Reports, Huddles, and Swapmeets. While I circulate and work with teams, I make it a priority to ask them where they are in answering the goal of the lesson. More often than not, teams have something to contribute towards answering the day’s question, and I ask them to get a marker and add their thoughts on the wall. This is where I have made my most progress as a teacher. As I shift from team to team, I keep in mind the goal of the lesson and incorporate that into my line of questioning. And by having the goal of the lesson on the back wall with student evidence of learning, I am able to use that with struggling teams. For example, I may point to something on the wall and ask, “What do you think that means?” or “Does that begin to answer today’s question?” This gives teams a chance to think and share their thoughts during the lesson. Universally, we can all agree that this approach is most powerful because it is student work, not mine.
Here are some examples of what it might look like:

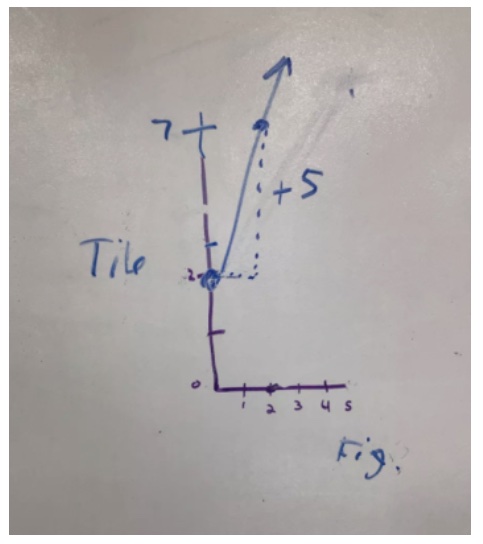
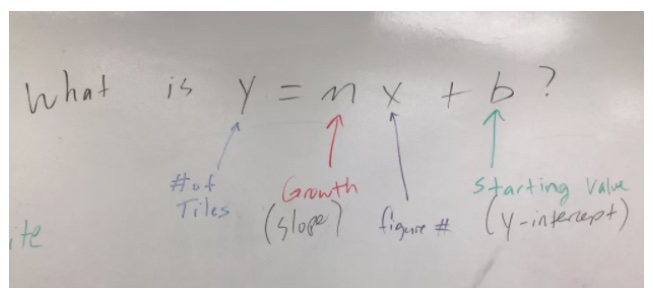
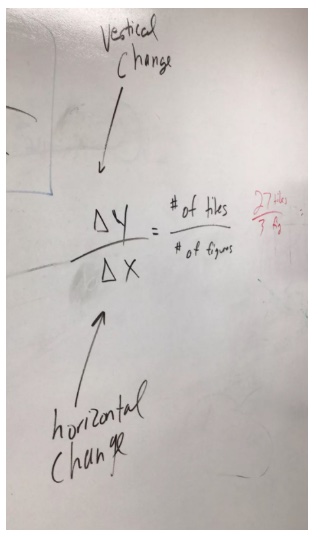
As I circulate, I file away who wrote what and how that would best be sequenced to share at the end of class. Sometimes, I see students answering the goal of the lesson in their Toolkit before closure. To me, that is quite potent because they trust what their classmates wrote.
At the end of class, we have students get their Toolkit out from under their book and I tell them it is time to answer the goal of the lesson.
As we look at each item written, I call on students to read what they wrote and explain what it means. There are times when I correct something on the wall, but I typically try to do this before closure. Also, there are days when students or I add something to the wall during closure that completes our answer to the question.
When we start or end a lesson, I often tell the class that if they can answer the question partway or completely they have made progress towards the goal of the lesson. It does not matter if they read something in their book, if their teammate said something or if they heard it or read it during closure; this demonstrates a growth mindset and progress towards understanding and learning
The days I feel are the most successful are days when everything on the back wall is student hand-writing and they can explain it all during closure. Not every day ends up that way, but I feel it gives us the best chance to be successful in reaching the goal of the lesson.

