January 2025

In my journey of observing classrooms as a CPM Professional Learning Specialist during Implementation Support Visits, I have had the privilege of witnessing a wide range of inspiring, practical, and high-impact teaching practices across intermediate, middle, and high school levels. From sixth through twelfth grade, these observations have showcased the dedication of newly implementing teachers and the collaboration of their students. I have seen a very practical, intentional, and flexible use of routines and strategies in action: support for multilingual learners, thoughtful use of team roles, effective integration of textbooks and vertical non-permanent surfaces (VNPS), community circles, and innovative use of devices. Alongside these practices, I have witnessed so much growth and reflection on teacher beliefs, classroom circulation, student collaboration, lesson pacing, and so much more. Each of these moments has offered valuable insights into the art of teaching that I would like to share as potential reminders or sources of inspiration. 

This article highlights the practices of seven teachers and the impact some of their decisions and routines have had on both their teaching and their students’ learning. 

Improving Student Engagement in High School Math Classrooms 

Tarilyn Greenfield, Core Connections Algebra 2, Oregon High School, Oregon, WI
This was my third observation of Tarilyn’s class across the last two school years. I saw some pretty big changes from last year to this year, so I asked Tarilyn to talk about how the changes she has made to team roles and textbooks have impacted her classroom. 

+ Use of Roles (Tarilyn): 
I was concerned that my high school students would resist the implementation of Team Roles, but that hasn’t been the case. Two major shifts have occurred in my classroom as a result of team roles. One, the transition time from task to task has dramatically reduced. Students are no longer waiting for someone else to volunteer to read, grab the resources, etc. With specific jobs, the work begins more quickly. Two, new leaders are starting to emerge within the classroom. By giving voice to each student in a specified role, students who are typically quieter are now given the opportunity to take the lead. This is also giving students who constantly feel the pressure to be the group initiator a break from that role.  

+ Use of Textbooks (Tarilyn): 
Last year I used packets in my classroom, rather than the textbook. By transitioning to the text itself, I have felt relief not having to print resources regularly and feel like I can be more flexible with how I use the Study Team and Teaching Strategies in the classroom. Last year with the packets, students wanted to regularly do their work in the packet rather than the proposed activity. Now students are embracing the activities as it gives them a break from the text.
 
Using the text has also given me the opportunity to teach students how to organize their work in a notebook. I believe that this is an important skill as students continue their math education beyond high school. With a packet, students do not have to practice and refine this skill. 

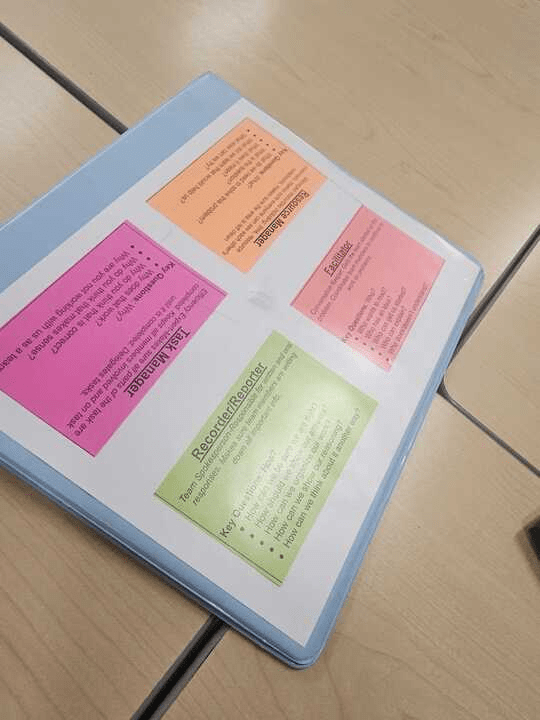
My (Danielle’s) Observation and Reflection: In Tarilyn’s first year implementing CPM, students were engaged and she was using strategies that fostered collaboration, but the shifts she made in year two to focus on the roles and use the textbook had a noticeable impact in the classroom culture. I witnessed students listening carefully to the thinking of their peers and interacting with all the members of their teams to ask clarifying questions and hold one another accountable. I also think that the relief and flexibility that Tarilyn described directly impacts her ability to plan and differentiate. Instead of using limited plan time to make edits and copies, she is able to focus on instruction and differentiation.

Matthew Krall, Core Connections Geometry, Oregon High School, Oregon, WI 

In my observation of Matt’s geometry classes, I have been able to see his implementation of Building Thinking Classrooms in his CPM geometry class. I asked him to reflect on the impact and use of Vertical Non–Permanent Surfaces (VNPSs), and this is what he had to say:   

+ Use of VNPS (Matthew):
This school year, students are working at VNPSs for almost every geometry lesson. This has been a change to the classroom structure for most students and requires intentional lessons to promote collaboration and community. Feedback from students has generally been very positive. During the beginning of the school year and throughout the first chapters of CPM, class time has been devoted to non-curricular tasks that develop norms for classroom collaboration. Students are learning to think and reason about math while building the foundation for the teamwork required of them in the curriculum. As a teacher, I am learning to give students opportunities to think, reason, and explore math, which takes time, is messy, and is often incomplete, as students need time and space to develop proficiency. While never perfect, each day I see students doing math, students see each other doing math, and students generally enjoy geometry. 

Some things of importance still need refinement:

• engaging students quickly at the start of class so that they are doing math almost immediately;
• using student work and voice for Closure at the end of class;
• taking time to teach students how to summarize their findings for the class; and
• developing extensions to learning tasks for groups that work faster. 

My (Danielle’s) Observation and Reflection: I can see the result of Matt’s reflection and collaboration with colleagues and the impact it has had on students. Each time I have been in his classroom, I have seen students collaborating effectively. Even though some students chose to work independently at some boards, before they knew it, they were asking others questions or observing other teams’ conversations and work as they naturally stopped and scanned the room for ideas. Knowledge was mobile, and the mathematical authority was in the hands of students.

Helping Middle School Math Teachers to Support Their Students

Kerrie Zacharski, Core Connections Course 1, Forest Edge Elementary School, Oregon, WI

Since meeting Kerrie when she started piloting Core Connections Course 1, I have reflected quite a bit with her about the impact CPM has had on her and her students. I asked her to share more about her experience.

+ Teams (Kerrie):
When I was first introduced to the team structure for teaching at the CPM training, I was very skeptical. How in the world am I going to get 6th graders to actually talk about math, let alone work together to solve problems? Danielle assured me it would work—trust the process. So, I set up my math teams, taught them about the roles, and we practiced using the sentence starters and questions on their role cards. It took a bit of encouragement and practice, but it worked! I was truly amazed at the math talk that happened. Actually talking, and sometimes arguing, about strategies and solutions! I was amazed and excited! It really does give everyone a voice and entrance point. Trust the process!

My (Danielle’s) Observation and Reflection:
In her classroom, I have seen 6th graders use their roles with fidelity and hold one another accountable. This has allowed Kerrie to focus on her circulation, questioning students to check for understanding or extend their thinking. During her circulation, she has also been able to provide feedback to students and teams on their collaboration or pause to model and foster collaboration among team members.

Stephanie Ostry, Core Connections Course 1, Rome Corners Intermediate, Oregon, WI

I have had the pleasure of observing in Stephanie’s classroom four times across the last couple of years as she piloted for her district, and in the first year of adopting CPM’s Core Connections series. I asked her to talk more about the GPS Study Team and Teaching Strategy pictured here that she uses daily in her classroom.

+ Use of GPS Study Team and Teaching Strategy (STTS) and Red Light, Green Light STTS (Stephanie): 
I have students move their location, and sometimes I draw lines for the check-in points where they have to have a red cup to move on. It is an easy way for me to see where each group is in the lesson. I can check in with groups that haven’t moved nearly as far to see if they are stuck or just off task. This strategy is a motivator for many groups. Teams can see if they are behind, and it helps keep them a bit more focused. As a bonus, this strategy allows movement for some of the students to go and move the marker to the next question.

My (Danielle’s) Observation and Reflection:
I saw these strategies benefit both the students AND the educators in the room firsthand. While students were given the opportunity to share the math authority and productively struggle without the teacher taking over the thinking, the teacher was able to formatively assess, circulate purposefully, and differentiate for learners by providing just-in-time support. I observed students collaborating and depending on one another, asking questions of one another and engaging in mathematical discourse. At the same time, the teacher was able to monitor and question the thinking of students and teams, and focus on some teams more than others as needed.

Emily Zaborsky, Core Connections Course 1 and Core Connections Course 2, Rome Corners Intermediate, Oregon, WI

Last year, Emily taught Core Connections Course 1 for the first time, and this year, she moved up with her students to teach Core Connections Course 2 for the first time. Over the last two years, her use of roles and a couple of key Study Team and Teaching Strategies has had a huge impact on her class, so I asked her to share her take on the team roles and her favorite strategies.

+ Classroom Routines (Emily):
I do groups of three (recorder/reporter, task manager, facilitator). I made my own picture cards for random groups. When they get to the group, the chair they pick corresponds to their role. They are asked to pick a different role with each move. I have the definition of the role along with key questions to ask posted on the wall so they are always visible.

I ask a different role each day to “check” for completed Review & Preview at the start of class and initiate the discussion at their table about their answers/thinking. I go around table to table and ask that person how many stickers (stickers = tried each Review & Preview problem) they need, and the person distributes the stickers. Review & Preview is a competition “grade” in my class. After they go through them at the table and I am done circulating, we go over a few together. I am trying to follow their lead and talk about the ones that they had questions on as a group. 

The students shared that they like the routine of CPM. They know what to expect each day as far as how the lessons are structured. This is important to me to help students feel successful. I have always been a very routine-based teacher, and the structure of the curriculum blends well with my classroom expectations.

+ Use of the Huddle Study Team and Teaching Strategy (Emily):
The first STTS that I tackled was the Huddle. I noticed when I was circulating that groups would have the same misconceptions or questions. In the past, I would have noticed this, stopped everyone, told the whole class the same thing at the same time, and usually modeled something on the whiteboard. I saw the Huddle as an opportunity to break this cycle and empower the students to help each other. Now when I want to share something with everyone, I call a Huddle. I always rotate through the roles so anyone can be called up. We meet at my front table and I always try to write something on my mini whiteboard that captures what we are discussing. Then, when I send them back to their tables, they share what we discussed. They are welcome to bring their entire group back to my whiteboard and use this resource to facilitate the discussion with their group. I also usually stick around by the front table to be there if the Huddle leader needs support when they bring their group back up.

The second STTS that I have started to use regularly is Think–Ink–Pair–Share. I try to use this one at the start of lessons. I have noticed that in some groups, the same person shares their ideas first. I use this STTS to break that cycle. It allows all students to have some independent thinking time and then writing time before the whole group starts working. Students have shared they like this one because they feel like they have an idea ready to share, and they do not have to be the fastest person to think of it at their table.

When I asked the students which one they liked the best in math class, they said I Spy was their favorite. They liked being able to see another team’s ideas if they felt stuck.

+ Takeaways:
I think one of my biggest takeaways is to do every lesson problem and Review & Preview problem before I teach the lesson. It helps me pick up on things that might be worded differently than expected and a general sense of how long the problems might take. The mathcast videos for each lesson are also helpful, with good reminders to try out the different STTS.

My (Danielle’s) Observation and Reflection:
In this classroom, the daily use of roles and STTS has now become more routine for both the teacher and students. Students know what to expect and regularly use their roles to support one another and collaborate as they read and make sense of the problems from the textbook. Something that stands out to me when I am in this classroom is that the teacher is not always asking or answering questions but often observing and listening. This is, in my opinion, an underutilized intentional teacher move. This teacher is able to recognize that a team is functioning and making progress, and asking a question may interrupt their flow. However, through her circulation, she is able to assess and determine whether students need some just-in-time support through the use of a Huddle, an all-time CPM teacher favorite.

Middle School Math Classrooms That Take Intentional Time for Growth

Peter Trapp, Inspiring Connections Course 2, Nature Hill Intermediate, Oconomowoc, WI 

Although this was only my first observation of Peter’s class, I have read his previous newsletter articles and work with CPM’s Teacher Research Corps about restorative practices, and they helped me tremendously in my own classroom and instruction. In his classroom, I saw “Math Minds Mingle” in action with seventh graders, and I wanted to invite him to share more about his implementation of community circles.

+ Community Circles:
I like using community circles in my classroom at times. I think it is important to let every child be given the opportunity to share a personal thought with the class. I have had students raise their hands to share while sitting at their desks, but it is easier for a child to never share with that model, because they just have to sit there and not raise their hand. The advantage of the circle is that there is an implied expectation that everyone shares. The talking piece goes around the circle and when it comes to you, this is your opportunity. You can pass, but now, opting out requires effort. 

Establishing clear expectations of the circle will set you up for an environment that encourages empathy and connectedness. 

1. Bring nothing extra to the circle, just yourself and your chair.
2. You can sit next to the person of your choosing as long as you can follow all of these expectations.
3. Look at and listen to the person with the talking piece.
4. No side conversations are allowed.
5. The only person talking is the person with the talking piece.

I also like to bring in a talking piece with a personal story attached to it. I currently have a stuffed animal that my children loved to play with when they were little. I ask that the students treat Piggie with respect because it is important to me. Once you have this set up in your class, you not only have a way of building community, but also an avenue to discuss larger issues that your class is having. 

My (Danielle’s) Observation and Reflection:
I was able to see an immediate impact as a result of this community circle. Although it takes up some of your class time, it is one of those examples of ‘go slow to go fast,’ as it helps establish a safe environment built on trust and rapport. After using the community circle to launch the lesson, I saw students taking risks, sharing their ideas, and growing in their mathematical understanding. Do not be scared to give it a try, or reach out for more support or tips.

Gina Perone, Inspiring Connections Course 3, Nature Hill Intermediate, Oconomowoc, WI

Students and teachers are within the first couple of years of implementing CPM’s newest series, Inspiring Connections. I have been able to visit Gina’s classroom and see the new curriculum in action, and I asked her to share about her experience and how she has been able to foster a collaborative environment in her classroom.

+ Holding Students to High Expectations and Showing Belief in Them as Mathematicians:
In the first few days of school, I make it clear to my students that I have high expectations for each of them. I tell them upfront that success in math is not necessarily about innate talent, but about hard work and a positive attitude. I promise students that if they give their best effort, the results will follow. I truly believe in their potential and make it my mission to help them build confidence and grow as mathematicians, regardless of where they start the year. It is fun to see students tackling new challenges with increased self-assurance. The most fulfilling part of my job is helping students develop the life skills of being critical thinkers and problem-solvers.

+ Circulation Around the Classroom:
This is a crucial part of my teaching approach for several reasons. It allows me to ensure that students are on track and gives me the opportunity to answer any questions they may have. However, the most rewarding aspect is being able to see the problem-solving process through a student lens. It never ceases to amaze me how students approach problems in a unique way, yet often arrive at the correct answer. Watching them navigate through different strategies deepens my understanding of their thinking and helps me adjust my teaching to better support their individual learning needs. It is a constant reminder of the diversity of thought in the classroom and the value of fostering creative problem-solving.

+ Letting Teams Work at Different Paces:
I believe in allowing student teams to work at their own paces, understanding that each student’s learning journey is unique. I do not feel the need to call students together to debrief after every math problem (unless I notice something going awry) because I trust that some students are ready to move forward while others may need more time to process and practice. This gives me the flexibility to focus more intently on students who may need additional support. By allowing students to progress at their own pace, I can provide a more individualized learning experience that fosters both confidence and growth for every student in the classroom.

+ Use of One Device Per Team:
The curriculum sometimes requires students to be online. We use one device per team (or occasionally two if the activity involves working closely with an elbow partner). Since many students arrive at school with uncharged devices, the one-device-per-team setup is often a practical necessity. This approach minimizes the need for constant monitoring of individual computers, which in turn allows me to focus more on guiding students through the lesson. It also keeps students on task and working together in a collaborative way rather than becoming distracted by individual screens. Additionally, having one device per table saves valuable space, giving students more room to keep their Mathematician’s Notebooks, math tools, and other resources readily available. This setup encourages both organization and teamwork, allowing students to engage effectively with the content and with one another.

My (Danielle’s) Observation and Reflection:
In her 8th grade classroom, Gina has a community established on high expectations that are supported by her classroom circulation and belief in her students. She clearly explains to students what the expectations are and why. If you have ever read about being a Warm Demander in Culturally Relevant Teaching and the Brain by Zaretta Hammond and thought about what that looks like in practice, Gina embodies it. It is not always easy to relinquish control and let teams work at different paces, as this is often more challenging for the teacher to manage. I know this did not happen overnight, but it has really moved the onus onto students and teams and helped shift students from dependent to independent learners.

I hope the reflections and experiences shared here can provide you with at least one of the following:

• relief as you probably find something you can relate to; 
• insight into the importance of reflection and the choices we make as teachers in the classroom; 
• inspiration to try out something new, or set a goal for yourself or your students; 
• permission to let go of old habits and embrace something new; or
• reassurance that you are not alone, and you have colleagues near and far to collaborate with and support your growth.

I remember my first years implementing CPM, and I remember how much work it was, as well as how rewarding it was. Throughout our professional learning, CPM always says that change takes time, effort, and support. So please, give yourself some grace and space, remind yourself that you and your students can do this, and know that you are really, truly not alone. Teaching this way may not always be easy, but it is definitely worth it.