









Core ideas are synthesized in “Math Notes” boxes, placed purposefully, often falling one or more lessons after the initial introduction of a concept. This allows students time to explore and build conceptual understanding of an idea before they are presented with a formal definition, algorithm or summary of a mathematical concept.
Checkpoints indicate to students where fluency with a skill should occur. Each checkpoint problem has the topic clearly labeled and the solution. Checkpoints also offer examples with detailed explanations, complete solution of the checkpoint problem, and more practice problems with answers included.

© 1989-2025 CPM EDUCATIONAL PROGRAM All rights reserved. CPM Educational Program is a 501(c)(3) educational nonprofit corporation.
LEARNING LOG
Write a Learning Log entry to summarize what you learned today about the Giant One and its uses. Include examples of how the Giant One is used. Title this entry “The Giant One and Equivalent Fractions” and label it with today’s date.

LEARNING LOG
Make a rectangle from any number of tiles. Your rectangle must contain at least one of each of the following tiles: x^2, y^2 , x, y and xy. Sketch your rectangle in your Learning Log and write its area as a product and as a sum. Explain how you know that the product and sum are equivalent. Title this entry “Area as a Product and as a Sum” and label it with today’s date.

2.3.4
Defining Concavity
4.4.1
Characteristics of Polynomial Functions
5.2.6
Semi-Log Plots
5 Closure
Closure How Can I Apply It? Activity 3
9.3.1
Transition States
9.3.2
Future and Past States
10.3.1
The Parametrization of Functions, Conics, and Their Inverses
10.3.2
Vector-Valued Functions
11.1.5
Rate of Change of Polar Functions
Section 1.1
1.1.1 Solving Puzzles in Teams
1.1.2 Investigating the Growth of Patterns
1.1.3 Multiple Representations of Functions
Section 1.2
1.2.1 Function Machines
1.2.2 Functions
1.2.3 Domain and Range
Section 1.3
1.3.1 Rewriting Expressions with Exponents
1.3.2 Zero and Negative Exponents
Chapter Closure
Section 2.1
2.1.1 Seeing Growth in Linear Functions
2.1.2 Comparing Δy and Δx
2.1.3 Slope
2.1.4 y= mx+ band More on Slope
Section 2.2
2.2.1 Modeling Linear Functions
2.2.2 Rate of Change
2.2.3 Equations of Lines in a Situation
2.2.4 Dimensional Analysis
Section 2.3
2.3.1 WritingtheEquation of a Line Given theSlope and a Point
2.3.2 Writingthe Equation of a Line Through Two Points
2.3.3 Writing y= mx+ b from Graphs and Tables
Chapter Closure
Section 3.1
3.1.1 Spatial Visualization and Reflections
3.1.2 Rotations and Translations
3.1.3 Slopes of Parallel and Perpendicular Lines
3.1.4 Defining Rigid Transformations
3.1.5 Using Transformations to Create Polygons
3.1.6 Symmetry
Section 3.2
3.2.1 Modeling Area and Perimeter with Algebra Tiles
3.2.2 Exploring an Area Model
3.2.3 Multiplying Polynomials and the Distributive Property
Section 3.3
3.3.1 Multiple Methods for Solving Equations
3.3.2 Fraction Busters
3.3.3 Solving Exponential and Complex Equations
Chapter Closure
Section 4.1
4.1.1 Line of Best Fit
4.1.2 Residuals
4.1.3 Upper and Lower Bounds
4.1.4 Least Squares Regression Line
Section 4.2
4.2.1 Residual Plots
4.2.2 Correlation
4.2.3 Association is Not Causation
4.2.4 Interpreting Correlation in Context
Chapter Closure
Section 5.1
5.1.1 Representing Exponential Growth
5.1.2 Rebound Ratios
5.1.3 The Bouncing Ball and Exponential Decay
Section 5.2
5.2.1 Generating and Investigating Sequences
5.2.2 Generalizing Arithmetic Sequences
5.2.3 Recursive Sequences
Section 5.3
5.3.1 ComparingGrowth in Tables and Graphs
5.3.2 Using Multipliers to Solve Problems
5.3.3 Comparing Sequences to Functions
Chapter Closure
Section 6.1
6.1.1 Working with Multi-Variable Equations
6.1.2 Summary of SolvingEquations
6.1.3 Solving Word Problems by Using Different Representations
6.1.4 Solving WordProblems by Writing Equations
Section 6.2
6.2.1 Solving Systems of Equations Using the Equal ValuesMethod
6.2.2 Solving Systems of Equations Using Substitution
6.2.3 Making Connections: Systems andMultiple Representation
Section 6.3
6.3.1 Solving Systems Using Elimination
6.3.2 More Elimination
6.3.3 Making Connections: Systems, Solutions, and Graphs
Section 6.4
6.4.1 Choosing a Strategy for Solving a System
6.4.2 Pulling it all Together
Chapter Closure
Section 7.1
7.1.1 Defining Congruence
7.1.2 Conditions for Triangle Congruence
7.1.3 Creating a Flowchart
7.1.4 Justifying Triangle CongruenceUsing Flowcharts
7.1.5 More Conditions for Triangle Congruence
7.1.6 Congruence of Triangles Through Rigid Transformations3947.1.7More Congruence Flowcharts
Section 7.2
7.2.1 Studying Quadrilaterals on a Coordinate Grid
7.2.2 Coordinate Geometry and Midpoints4
7.2.3 Identifying Quadrilaterals on a Coordinate Grid
Chapter Closure
Section 8.1
8.1.1 Investigating
8.1.2 Multiple Representations of Exponential Functions
8.1.3 More Applications of Exponential Functions
8.1.4 Exponential Decay
8.1.5 Graph →Equation
8.1.6 Completing the Multiple Representations Web
Section 8.2
8.2.1 Curve Fitting
8.2.2 Curved Best-Fit Models
8.2.3 Solving a System of Exponential Functions Graphically
Chapter Closure
Section 9.1
9.1.1 Solving Linear, One-Variable Inequalities
9.1.2 More Solving Inequalities
9.1.3 Solving Absolute Value Equations and Inequalities
Section 9.2
9.2.1 Graphing Two-Variable Inequalities
9.2.2 Graphing Linear and Nonlinear Inequalities
Section 9.3
9.3.1 Systems of Inequalities
9.3.2 More Systems of Inequalities
9.3.3 Applying Inequalities to Solve Problems
Chapter Closure
Section 10.1
10.1.1 Association in Two-Way Tables
10.1.2 Investigating Data Representations
10.1.3 Comparing Data
10.1.4 Standard Deviation
Section 10.2
10.2.1 Transforming Functions
10.2.2 Arithmetic Operations with Functions
10.2.3 Proving Linear and Exponential GrowthPatterns
Chapter Closure
Section 11.1 11.1.1 Introduction to Constructions
11.1.2 Constructing Bisectors
11.1.3 More Explorations with Constructions
Section 11.2
11.2.1 Solving Work and Mixing Problems
11.2.2 Solving Equations and Systems Graphically
11.2.3 Using a Best-Fit Line to Make a Prediction
11.2.4 Treasure Hunt
11.2.5 Using Coordinate Geometry and Constructions to Explore Shapes
11.2.6 Modeling with Exponential Functions and Linear Inequalities
Chapter Closure
Section A.1
A.1.1 Exploring Variables and Expressions
A.1.2 Using Zero to Simplify Algebraic Expressions
A.1.3 Using Algebra Tiles to Compare Expressions
A.1.4 Justifying and Recording Work
A.1.5 Using Algebra Tiles to Solve for x
A.1.6 More Solving Equations
A.1.7 Checking Solutions
A.1.8 Determining the Number of Solutions
A.1.9 UsingEquations to Solve Problems
Appendix Closure
Checkpoint1: Solving Linear Equations, Part 1 (Integer Coefficients)
Checkpoint 2: Evaluating Expressions and the Order of Operations
Checkpoint 3: Operations with Rational Numbers
Checkpoint 4: Laws of Exponents and Scientific Notation
Checkpoint 5: Writing the Equation of a Line
Checkpoint 6A: Solving Linear Equations, Part 2 (Fractional Coefficients)
Checkpoint 6B: Multiplying Binomials and Solving Equations with Parentheses
Checkpoint 7: Interpreting Associations
Checkpoint 8A: Rewriting Equations with More Than One Variable
Checkpoint 8B: Solving Problems by Writing Equations
Checkpoint 9: Solving Linear Systems of Equations
Checkpoint 10: Determining Congruent Triangles
Checkpoint 11: The Exponential Web
Section 1.1
1.1.1 Attributes of Polygons
1.1.2 More Attributes of Polygons
Section 1.2
1.2.1 Making Predictions and Investigating Results
1.2.2 Perimeters and Areas of Enlarging Patterns
11.2.3 Area as a Product and a Sum
1.2.4 Describing a Graph
Section 1.3
1.3.1 Angle Pair Relationships
1.3.2 Angles Formed by Transversals
1.3.3 More Angles Formed by Transversals
1.3.4 Angles and Sides of a Triangle
Chapter Closure
Section 2.1
2.1.1 Triangle Congruence Theorems
2.1.2 Flowcharts for Congruence
2.1.3 Converses
2.1.4 Proof by Contradiction
Section 2.2
2.2.1 Dilations
2.2.2 Similarity
Section 2.3
2.3.1 Conditions for Triangle Similarity
2.3.2 Determining Similar Triangles
2.3.3 Applying Similarity
2.3.4 Similar Triangle Proofs
Chapter Closure
Section 3.1
3.1.1 Using an Area Model
3.1.2 Using a Tree Diagram
3.1.3 Probability Models
3.1.4 Unions, Intersections, and Complements
3.1.5 Expected Value
Section 3.2
3.2.1 Constant Ratios in Right Triangles
3.2.2 Connecting Slope Ratios to Specific Angles
3.2.3 Expanding the Trig Table
3.2.4 The Tangent Ratio
3.2.5 Applying the Tangent Ratio
Chapter Closure
Section 4.1
4.1.1 Introduction to Factoring Expressions
4.1.2 Factoring with Area Models
4.1.3 Factoring More Quadratics
4.1.4 Factoring Completely
4.1.5 Factoring Special Cases
Section 4.2
4.2.1 Sine and Cosine Ratios
4.2.2 Selecting a Trig Tool
4.2.3 Inverse Trigonometry
4.2.4 Trigonometric Applications
Chapter Closure
Section 5.1
5.1.1 Investigating the Graphs of Quadratic Functions
5.1.2 Multiple Representations of Quadratic Functions
5.1.3 Zero Product Property
5.1.4 Writing Equations for Quadratic Functions
5.1.5 Completing the Quadratic Web
Section 5.2
5.2.1 Perfect Square Equations
5.2.2 Completing the Square
5.2.3 More Completing the Square
5.2.4 Introduction to the Quadratic Formula
5.2.5 Solving and Applying Quadratic Equations
5.2.6 Introducing Complex Numbers
Chapter Closure
Section 6.1
6.1.1 Special Right Triangles
6.1.2 Pythagorean Triples
6.1.3 Special Right Triangles and Trigonometry
6.1.4 Radicals and Fractional Exponents
Section 6.2
6.2.1 At Your Service
6.2.2 Angles on a Pool Table
6.2.3 Shortest Distance Problems
6.2.4 The Number System and Deriving the Quadratic Formula
6.2.5 Using Algebra to Find a Maximum
6.2.6 Analyzing a Game
Chapter Closure
Section 7.1
7.1.1 Explore-Conjecture-Prove
7.1.2 Properties of Rhombi
7.1.3 Two Column Proofs
7.1.4 More Geometric Proofs
7.1.5 Using SimilarTriangles to Prove Theorems
Section 7.2
7.2.1 Conditional Probability and Independence
7.2.2 More Conditional Probability
7.2.3 Applications of Probability
Chapter Closure
Section 8.1
8.1.1 Constructing Triangle Centers
Section 8.2
8.2.1 Angles of Polygons
8.2.2 Areas of Regular Polygons
Section 8.3
8.3.1 Area Ratios of Similar Figures
8.3.2 Ratios of Similarity
Section 8.4
8.4.1 A Special Ratio
8.4.2 Arcs and Sectors
8.4.3 Circles in Context
Chapter Closure
Section 9.1
9.1.1 Modeling Nonlinear Data
9.1.2 Parabola Investigation
9.1.3 Graphing Form of a Quadratic Function
9.1.4 Transforming the Absolute Value Function
Section 9.2
9.2.1 Quadratic Applications with Inequalities
9.2.2 Solving Systems of Equations
Section 9.3
9.3.1 Average Rate of Change and Projectile Motion5099.3.2Comparing the Growth of Functions
9.3.3 Piecewise-Defined Functions
9.3.4 Combining Functions
Section 9.4
9.4.1 Inverse Functions
Chapter Closure
Section 10.1
10.1.1 The Equation of a Circle
10.1.2 Completing the Square for Equations of Circles
10.1.3 The Geometric Definition of a Parabola
Section 10.2
10.2.1 Introduction to Chords
10.2.2 Angles and Arcs
10.2.3 Chords and Angles
10.2.4 Tangents
10.2.5 Tangents and Arcs
Chapter Closure
Section 11.1
11.1.1 Prisms and Cylinders
11.1.2 Volumes of Similar Solids
11.1.3 Ratios of Similarity
Section 11.2
11.2.1 Volume of a Pyramid
11.2.2 Surface Area and Volume of a Cone
11.2.3 Surface Area and Volume of a Sphere
Chapter Closure
Section 12.1
12.1.1 The Fundamental Counting Principle
12.1.2 Permutations
12.1.3 Combinations
12.1.4 Categorizing Counting Problems
Section 12.2
12.2.1 Using Geometry to CalculateProbabilities
12.2.2 Choosing a Model
12.2.3 The Golden Ratio
12.2.4 Some Challenging Probability Problems
Chapter Closure
Checkpoint 1: Solving Problems with Linear and Exponential Relationships
Checkpoint 2: Calculating Areas and Perimeters of Complex Shapes
Checkpoint 3: Angle Relationships in Geometric Figures
Checkpoint 4: Solving Proportions and Similar Figures
Checkpoint 5: Calculating Probabilities
Checkpoint 7: Factoring Quadratic Expressions
Checkpoint 8: Applying Trigonometric Ratios and the Pythagorean Theorem
Checkpoint 9: The Quadratic Web
Checkpoint 10: Solving Quadratic Equations
Checkpoint 11: Angle Measures and Areas of Regular Polygons
Checkpoint 12: Circles, Arcs, Sectors, Chords, and Tangents
Section 1.1
1.1.1 Solving a Function Puzzle in Teams
1.1.2 Using a Graphing Calculator to Explore a Function
1.1.3 Function Investigation
1.1.4 Combining Linear Functions
Section 1.2
1.2.1Representing Points of Intersection
1.2.2 Modeling a Geometric Relationship
1.2.3 Describing Data
Chapter Closure
Section 2.1
2.1.1 Transforming Quadratic Functions
2.1.2 Modeling with Parabolas
Section 2.2
2.2.1 Transforming Other Parent Graphs
2.2.2 Describing (h,k) for Each Family of Functions
2.2.3 Transformations of Functions 2.2.4 TransformingNon-Functions
2.2.5 Developing a Mathematical Model
Section 2.3
2.3.1 Completing the Square
Chapter Closure
Section 3.1
3.1.1 Strategies for Solving Equations
3.1.2 Solving Equations Graphically
3.1.3 Multiple Solutions to Systems of Equations
3.1.4 Using Systems of Equations to Solve Problems
Section 3.2
3.2.1 Solving Inequalities with One or Two Variables
3.2.2 Using Systems to Solve a Problem
3.2.3 Applications of Systems of Inequalities
3.2.4 Using Graphs to DetermineSolutions
Chapter Closure
Section 4.1
4.1.1 Survey Design
4.1.2Samples and the Role of Randomness
4.1.3 Bias in Convenience Samples
Section 4.2
4.2.1 Testing Cause and Effect with Experiments
4.2.2 Conclusions from Studies
Section 4.3
4.3.1Relative Frequency Histograms
4.3.2 The Normal Probability Density Function
4.3.3 Percentiles
Section 4.4
4.4.1 Cross-Sections and Solids of a Revolution
4.4.2 Modeling with Geometric Solids
4.4.3 Designing to Meet Constraints
Chapter Closure
Section 5.1
5.1.1 “Undo” Equations
5.1.2 Using a Graph to Find an Inverse
5.1.3 More Inverse Functions
Section 5.2
5.2.1 TheInverse of an Exponential Function
5.2.2 Defining the Inverse of an Exponential Function
5.2.3 Investigating the Family of Logarithmic Functions
5.2.4 Transformations of Logarithmic Functions
Chapter Closure
Section 6.1
6.1.1 Simulations of Probability
6.1.2 More Simulations of Probability
6.1.3 Simulating Sampling Variability
Section 6.2
6.2.1 Statistical Test Using Sampling Variability
6.2.2 Variability in Experimental Results
6.2.3 Quality Control
6.2.4 Statistical Process Control
Section 6.3
6.3.1 Analyzing Decisions and Strategies
Chapter Closure
Section 7.1
7.1.1 Using Logarithms to Solve Exponential Equations
7.1.2 Investigating the Properties of Logarithms
7.1.3 Writing Equations of Exponential Functions
7.1.4 An Application of Logarithms
Section 7.2
7.2.1 Determining Missing Parts of Triangles
7.2.2 Law of Sines
7.2.3 Law of Cosines
7.2.4 The Ambiguous Case
7.2.5 Choosing a Tool
Chapter Closure
Section 8.1
8.1.1 Sketching Graphs of Polynomial Functions
8.1.2 More Graphs of Polynomial Functions
8.1.3 Stretch Factors for Polynomial Functions
Section 8.2
8.2.1 Writing Equations Using Complex Roots
8.2.2 More Real and Complex Roots
Section 8.3
8.3.1 Polynomial Division
8.3.2 Factors and Rational Zeros
8.3.3 An Application of Polynomials
8.3.4 Special Cases of Factoring
Chapter Closure
Section 9.1
9.1.1 Introductions to Periodic Models
9.1.2 Graphing the Sine Functions
9.1.3 Unit Circle ↔Graph
9.1.4 Graphing and Interpreting the Cosine Function
9.1.5 Defining a Radian
9.1.6 Building a Unit Circle
9.1.7 The Tangent Function
Section 9.2 9.2.1 Transformations of y= sin(x)
9.2.2 One More Parameter for a Periodic Function
9.2.3 Period of a Trigonometric Function
9.2.4 Graph ↔Equation
Chapter Closure
Section 10.1
10.1.1 Introduction to Arithmetic Series
10.1.2 More Arithmetic Series
10.1.3 General Arithmetic Series
10.1.4 Summation Notation and Combinations of Series
10.1.5 Mathematical Induction
Section 10.2
]10.2.1 Geometric Series
10.2.2 Infinite Series
Section 10.3
10.3.1 Using a Binomial Probability Model
10.3.2 Pascal’s Triangle and the Binomial Theorem
10.3.3 The Number e
Chapter Closure
Section 11.1
11.1.1 Simplifying Rational Expressions
11.1.2 Multiplying and Dividing Rational Expressions
11.1.3 Adding and Subtracting Rational Expressions
11.1.4 Operations with Rational Expressions
Section 11.2
11.2.1 Creating a Three-Dimensional Model
11.2.2 Graphing Equations in Three Dimensions
11.2.3 Solving Systems of Three Equations with Three Variables
11.2.4 Using Systems of Three Equations for Curve Fitting
Chapter Closure
Section 12.1
12.1.1 Analyzing Trigonometric Equations
12.1.2 Solutions to TrigonometricEquations
12.1.3 Inverses of Trigonometric Functions
12.1.4 Reciprocal Trigonometric Functions
Section 12.2
12.2.1 Trigonometric Identities
12.2.2 Proving Trigonometric Identities
12.2.3 Angle Sum and Difference Identities
Chapter Closure
Checkpoint 2: Solving Quadratic Equations
Checkpoint 3: Function Notation and Describing a Function
Checkpoint 4: Expressions with Integer and Rational Exponents
Checkpoint 5: Transformations of Functions
Checkpoint 6: Solving Complicated Equations and Systems
Checkpoint 7: Solving and Graphing Inequalities
Checkpoint 8: Determining the Equation for the Inverse of a Function
Checkpoint 9A: Solving Equations with Exponents
Checkpoint 9B: Rewriting Expressions and Solving Equations with Logarithms
Checkpoint 10: Solving Triangles
Checkpoint 11: Roots and Graphs of Polynomial Functions
Checkpoint 12: Periodic Functions
Sección 1.1
1.1.1 Resolución de acertijos en equipo
1.1.2 Investigar el crecimiento de patrones
1.1.3 Investigación de los gráficos de funciones cuadráticas
Sección 1.2
1.2.1 Descripción de un gráfico
1.2.2 Raíz cúbica y funciones de valor absoluto
1.2.3 Máquinas de funciones
1.2.4 Funciones
1.2.5 Dominio y rango
Resumen del Capítulo
Sección 2.1
2.1.1 Observación del crecimiento en las representaciones lineales
2.1.2 Pendiente
2.1.3 Comparación de Δy y Δx
2.1.4 y = mx + b y más información sobre pendientes
Sección 2.2
2.2.1 Pendiente como movimiento
2.2.2 Tasa de cambio
2.2.3 Ecuaciones de rectas en situaciones dadas
Sección 2.3
2.3.1 Hallar una ecuación a partir de la pendiente y un punto
2.3.2 Cómo hallar la ecuación de una recta que atraviesa dos puntos
Actividad de extensión Cómo hallar y = mx + b a partir de gráficos y tablas
Resumen del Capítulo
Sección 3.1
3.1.1 Simplificación de expresiones exponenciales
3.1.2 Exponentes negativos eiguales a cero
Sección 3.2
3.2.1 Ecuaciones ↔ azulejos algebraicos
3.2.2 Exploración de modelos de área
3.2.3 Multiplicación de binomios y la Propiedad distributiva
3.2.4 Uso de rectángulos genéricos para multiplicar
Sección 3.3
3.3.1 Resolver ecuaciones conmultiplicaciones y valores absolutos
3.3.2 Trabajando con ecuaciones con múltiples variables
3.3.3 Resumen de la resolución de ecuaciones
Resumen del Capítulo
Sección 4.1
4.1.1 Resolución de
problemas de palabras con
4.1.2 ¿Una ecuación o dos
Sección 4.2
4.2.1 Resolución de sistemas de ecuaciones por sustitución
4.2.2 Realizar conexiones: sistemas, soluciones, y gráficos
4.2.3 Resolución de sistemas por medio de la eliminación
4.2.4 Más información sobre el método de eliminación
4.2.5 Selección de una estrategia para la resolución de sistemas
Sección 4.3
4.3.1 Unificar todoResumen del Capítulo
| Opening | 5.OP | Chapter Opening |
|---|---|---|
| Section 5.1 | 5.1.1 | Representing Fraction Multiplication |
| 5.1.2 | Describing Parts of Parts | |
| 5.1.3 | Calculating Parts of Parts | |
| 5.1.4 | Multiplying Mixed Numbers | |
| Section 5.2 | 5.2.1 | Making Sense of Decimal Multiplication |
| 5.2.2 | Fraction Multiplication Number Sense | |
| Section 5.3 | 5.3.1 | Rearranging Areas |
| 5.3.2 | Area of a Parallelogram | |
| 5.3.3 | Area of a Triangle | |
| 5.3.4 | Area of a Trapezoid | |
| Closure | 5.CL | Chapter Closure |
| Section 5.4 | Mid-Course Reflection Activities |
Sección 6.1
6.1.1 Recta de mejor ajuste
6.1.2 Valores residuales
6.1.3 Cota superior y cota inferior
6.1.4 Línea de regresión de mínimos cuadrados
Sección 6.2
6.2.1 Diagramas de valor residual
6.2.2 Correlación
6.2.3 Asociación no es causalidad
6.2.4 Interpretación de la correlación en contexto
6.2.5 Modelos de mejor ajuste curvos
Resumen del Capítulo
Sección 7.1
7.1.1 Investigar y = b x
7.1.2 Múltiples representaciones de funciones exponenciales
7.1.3 Más aplicaciones del crecimiento exponencial
7.1.4 Decaimiento exponencial
7.1.5 Gráfico → ecuación
7.1.6 Completar la red de representaciones múltiples
Sección 7.2
7.2.1 Curvas de ajuste y exponentes fraccionarios
7.2.2 Más curvas de ajuste
7.2.3 Resolución gráfica de un sistema de funciones exponenciales
Resumen del Capítulo
Sección 8.1
8.1.1 Introducción a la factorización de expresiones cuadráticas
8.1.2 Factorización con rectángulos genéricos
8.1.3 Factorización en casos especiales
8.1.4 Factorizar completamente
8.1.5 Atajos de factorización
Sección 8.2
8.2.1 Múltiples representaciones de funciones cuadráticas
8.2.2 Propiedad de producto cero
8.2.3 Más formas de hallar puntos de corte con el eje x
8.2.4 Completar la red cuadrática
8.2.5 Completar cuadrados
Resumen del Capítulo
Sección 9.1
9.1.1 Resolución de ecuaciones cuadráticas
9.1.2 Introducción a la Fórmula cuadrática
9.1.3 Más ecuaciones cuadráticas
9.1.4 Elección de una estrategia
Sección 9.2
9.2.1 Resolución de desigualdades lineales de una variable
9.2.2 Más desigualdades
Sección 9.3
9.3.1 Graficación de desigualdades lineales con dos variables
9.3.2 Graficación de desigualdades lineales y no lineales
Sección 9.4
9.4.1 Sistemas de desigualdades
9.4.2 Más sistemas de desigualdades
9.4.3 Aplicación de desigualdades a la resolución de problemas
Resumen del Capítulo
Sección 10.1
10.1.1 Asociaciones en tablas de doble entrada
Sección 10.2
10.2.1 Resolver reescribiend
10.2.2 Rompe fracciones
10.2.3 Múltiples métodos de resolución de ecuaciones
10.2.4 Determinar la cantidad de soluciones
10.2.5 Derivación de la Fórmula cuadrática y el sistema numérico
10.2.6 Más información sobre resolución y aplicaciones
Sección 10.3
10.3.1 Intersección de dos funciones
10.3.2 Cantidad de intersecciones de una parábola
10.3.3 Resolución de ecuaciones cuadráticas y con valores absolutos
Resumen del Capítulo
Sección 11.1
11.1.1 Transformación de funciones
11.1.2 Funciones inversas
Sección 11.2
11.2.1 Investigación de representaciones de datos
11.2.2 Comparación de datos
11.2.3 Desviación estándar
Sección 11.3
11.3.1 Uso de una recta de mejor ajuste para realizar predicciones
11.3.2 Búsqueda del tesoro de relaciones
11.3.3 Investigación de una función compleja
11.3.4 Uso del álgebra para hallar un máximo
11.3.5 Funciones exponenciales y desigualdades lineales
Resumen del Capítulo6
Sección A.1
A.1.1 Exploración de variables y agrupación de términos semejantes
A.1.2 Simplificación de expresiones combinando términos semejantes
A.1.3 Escritura de expresiones algebraicas
A.1.4 Uso del cero para simplificar expresiones algebraicas
A.1.5 Uso de azulejos algebraicos para simplificar expresiones algebraicas
A.1.6 Uso de azulejos algebraicos para comparar expresiones
A.1.7 Simplificación y registro del trabajo
A.1.8 Uso de azulejos algebraicos para resolver para
x
A.1.9 Más ecuaciones para resolver
Resumen del Apéndic
Sección1.1
1.1.1 Creación de una manta usando la simetría
1.1.2 Cómo hacer predicciones e investigar los resultados
1.1.3 Perímetro yárea de patrones de azulejos que se agrandan
1.1.4 Argumentos lógicos
1.1.5 Construcción de un caleidoscopio
Sección 1.2
1.2.1 Visualización espacial y reflexiones
1.2.2 Transformaciones rígidas: Rotaciones y traslaciones
1.2.3 Pendientes de rectas paralelas y perpendiculares
1.2.4 Definición de transformaciones
1.2.5 Uso de las transformaciones para crear formas
1.2.6 Simetría
Sección1.3
1.3.1 Atributos y características de las formas
1.3.2 Más características de las figuras
Resumen del Capítulo
Sección 2.1
2.1.1 Ángulos complementarios, suplementarios y opuestos por el vértice
2.1.2 Ángulos formados por transversales
2.1.3 Más ángulos formados por transversales
2.1.4 Ángulos de un triángulo
2.1.5 Aplicación de las relaciones entre ángulos1
Sección 2.2
2.2.1 Unidades de medida
2.2.2 Áreas de triángulos y figuras compuestas
2.2.3 Áreas de paralelogramos y trapecios
2.2.4 Alturas y áreas
Sección 2.3
2.3.1 Teorema de la desigualdad de un triángulo
2.3.2 El Teorema de Pitágoras
Resumen del Capítulo
Sección 3.1
3.1.1 Dilatación
3.1.2 Semejanzas
3.1.3 Uso de las razones de semejanza
3.1.4 Aplicaciones y notación
Sección3.2
3.2.1 Condiciones de semejanza de triángulos
3.2.2 Creación de un diagrama de flujo
3.2.3 Semejanza entre triángulos y congruencia
3.2.4 Más condiciones de semejanza de triángulos
3.2.5 Determinar semejanzas
3.2.6 Aplicación de la semejanza
Resumen del Capítulo
Sección4.1
4.1.1 Razones constantes en triángulos rectángulos
4.1.2 Relación entre razones de la pendiente y ángulos específicos
4.1.3 Ampliación de la tabla de trigonometría
4.1.4 La razón tangente
4.1.5 Aplicación de la razón tangente
Sección 4.2
4.2.1 Uso de un modelo de área
4.2.2 Uso de un diagrama de árbol
4.2.3 Modelos de probabilidad
4.2.4 Uniones, intersecciones y complementos
4.2.5Valor esperado
Resumen del Capítulo
Sección5.1
5.1.1 Razones seno y coseno
5.1.2 Elección de una herramienta de trigonometría
5.1.3 Trigonometría inversa
5.1.4 Aplicaciones trigonométricas
Sección5.2
5.2.1 Triángulos rectángulos especiales
5.2.2 Ternas pitagóricas
Sección 5.3
5.3.1 Cómo hallar las partes faltantes de los triángulos
5.3.2 Ley de los senos
5.3.3 Ley de los cosenos
5.3.4 Triángulos ambiguos(Optativo)
5.3.5 Elección de una herramienta
Resumen del Capítulo
Sección6.1
6.1.1Triángulos congruentes
6.1.2 Condiciones para congruencia de triángulos
6.1.3 Congruencia de triángulos a través de transformaciones rígidas3526.1.4Diagramas de flujo para congruencia
6.1.5 Recíprocos
Sección6.2
6.2.1 Ángulos sobre una mesa de pool
6.2.2 Investigar un triángulo
6.2.3 Creación de un modelomatemático
6.2.4 Análisis de un juego
6.2.5 Uso de transformaciones y simetría para diseñar copos de nieve
Resumen del Capítulo
Sección 7.1
7.1.1 Propiedades de un círculo
7.1.2 Construcción de un tetraedro
7.1.3 Problemas de distancia más corta
7.1.4 Uso de la simetría para el estudio de polígonos
Sección 7.2
7.2.1 Cuadriláteros especiales y demostraciones
7.2.2 Propiedades de los rombos
7.2.3 Más demostraciones con triángulos congruentes4297.2.4Más propiedades de los cuadriláteros
7.2.5 Demostraciones en dos columnas4387.2.6Explora-Conjetura-Demuestra
Sección 7.3
7.3.1 Estudio de cuadriláteros sobre una cuadrilla de coordenadas
7.3.2 Geometría en coordenadas y puntos medios
7.3.3 Cómo identificar cuadriláteros sobre una cuadrícula de coordenadas
Resumen del Capítulo
Sección 8.1
8.1.1 Molinillos y polígonos
8.1.2 Ángulos interiores de los polígonos
8.1.3 Ángulos de polígonos regulares
8.1.4 Conexiones de los ángulos de los polígonos regulares
8.1.5 Cómo calcular las áreas de polígonos regulares
Sección 8.2
8.2.1 Razones de área de figuras semejantes
8.2.2 Razones de semejanza
Sección 8.3
8.3.1 Una razón especial
8.3.2 Área y circunferencia de un círculo
8.3.3 Círculos en contexto
Resumen del Capítulo
Sección 9.1
9.1.1Sólidos tridimensionales
9.1.2 Volúmenes y áreasde superficies de los prismas
9.1.3 Prismas y cilindros
9.1.4 Volúmenes de sólidos similares
9.1.5 Razones de semejanza
Sección 9.2
9.2.1 Introducción a las construcciones5529.2.2Construcción de bisectrices
9.2.3 Más exploraciones con construcciones
9.2.4 Otras construcciones
Resumen del Capítulo
Sección 10.1
10.1.1 Introducción a las cuerdas
10.1.2 Ángulos y arcos
10.1.3 Cuerdas y ángulos
10.1.4 Tangentes y secantes
10.1.5 Resolver problemas con círculos
Sección 10.2
10.2.1 Probabilidad condicional e independencia’
10.2.2 Tablas de doble entrada
10.2.3 Aplicaciones de probabilidad
Sección10.3
10.3.1 El Principio fundamental de conteo
10.3.2 Permutaciones
10.3.3 Combinaciones
10.3.4 Categorizar problemas de conteo
10.3.5 Algunos problemas de probabilidad desafiantes
Resumen del Capítulo
Sección11.1
11.1.1 Sólidos platónicos
11.1.2 Pirámides
11.1.3 Volumen de una pirámide
11.1.4 Área de superficie y volumen de un cono
11.1.5 Área de superficie y volumen de una esfera
Sección 11.2
11.2.1 Coordenadas en una esfera
11.2.2 Tangentes y arcos
11.2.3 Relaciones de secantes y tangentes
Resumen del Capítulo
Sección 12.1
12.1.1 La ecuación de un círculo
12.1.2 Técnica de completar cuadrados para las ecuaciones de círculos
12.1.3 Introducción a las secciones cónicas
12.1.4 Graficación de una parábola usando el foco y la directriz
Sección 12.2
12.2.1 Uso de la geometría en coordenadas y las construcciones para explorar las formas
12.2.2 La Fórmula de los poliedros de Euler
12.2.3 La razón áurea
12.2.4 Uso de la geometría para hallar probabilidades
Resumen del Capítulo
Sección 1.1
1.1.1 Resolución de acertijos en equipo
1.1.2 Cómo usar una calculadora gráfica para explorar una función
1.1.3 Dominioy rango
1.1.4 Puntos de intersección en representaciones múltiples
Sección 1.2
1.2.1 Modelado de una relación geométrica
1.2.2 Investigación de funciones
1.2.3 La familia de funciones lineales
1.2.4 Reto de investigación de funciones
Resumen del Capítulo
Sección 2.1
2.1.1 Modelado de datos no lineales
2.1.2 Investigación sobre parábolas
2.1.3 Graficar una parábola sin una tabla
2.1.4 Reescribir en la forma de graficación
2.1.5 Modelación matemática con parábolas
Sección 2.2
2.2.1 Transformación de otros gráficos madre
2.2.2 Descripción de (h, k) para cada familia de funciones
2.2.3 Transformaciones de funciones
2.2.4 Transformación de ecuaciones que no son funciones
2.2.5 Transformación de funciones seccionadas
Resumen del Capítulo
Sección 3.1
3.1.1 Expresiones equivalentes
3.1.2 Reescribir expresiones y determinar equivalencias
3.1.3 Resolver reescribiendo
Sección 3.2
3.2.1 Investigación de funciones racionales
3.2.2 Simplificación de expresiones racionales
3.2.3 Multiplicación y división de expresiones racionales
3.2.4 Suma y resta de expresiones racionales1503.2.5Creación de nuevas funciones
Resumen del Capítulo
Sección 4.1
4.1.1 Estrategias de resolución de ecuaciones
4.1.2 Resolución de ecuaciones y sistemas en forma gráfica
4.1.3 Hallar múltiples soluciones a sistemas de ecuaciones
4.1.4 Uso de sistemas de ecuaciones para resolver problemas
Sección 4.2
4.2.1 Resolución de desigualdades con una o dos variables
4.2.2 Uso de sistemas para resolver un problema
4.2.3 Aplicación de los sistemas de desigualdades lineales
4.2.4 Uso de gráficos para hallar soluciones
Resumen del Capítulo
Sección 5.1
5.1.1 “Deshacer” ecuaciones
5.1.2 Usar un gráfico para hallar una inversa
5.1.3 Hallar inversas y justificar algebraicamente
Sección 5.2
5.2.1 Hallar la inversa de una función exponencial
5.2.2 Definir la inversa de una función exponencial
5.2.3 Investigar la familia de funciones logarítmicas
5.2.4 Transformaciones de funciones logarítmicas
5.2.5 Investigar composiciones de funciones
Resumen del Capítulo
Sección 6.1
6.1.1 Creación de un modelo tridimensional
6.1.2 Graficación de ecuaciones en tres dimensiones
6.1.3 Sistemas de tres ecuaciones variables
6.1.4 Resolución de sistemas de tres ecuaciones con tres incógnitas
6.1.5 Empleo de sistemas de tres ecuaciones para curvas de ajuste
Sección 6.2
6.2.1 Uso de logaritmos para resolver ecuaciones exponenciales
6.2.2 Investigación de las propiedades de los logaritmos
6.2.3 Escritura de ecuaciones de funciones exponenciales
6.2.4 Una aplicación de los logaritmos
Resumen del Capítulo
Sección 7.1
7.1.1 Introducción a los modelos cíclicos
7.1.2 Cómo graficar la función seno
7.1.3 Círculo de unidad↔Gráfico
7.1.4 Cómo graficar e interpretar la función coseno
7.1.5 Definición de radián
7.1.6 Construcción de un círculo de unidad
7.1.7 La función tangente
Sección 7.2
7.2.1 Transformaciones de y= sen x
7.2.2 Un parámetro más para una función cíclica
7.2.3 Período de una función cíclica
7.2.4 Gráfico↔Ecuación
Resumen del Capítulo
Sección 8.1
8.1.1 Cómo graficar funciones polinómicas
8.1.2 Más gráficos de polinomios
8.1.3 Factores de estiramiento para funciones polinómicas
Sección 8.2
8.2.1 Introducción a los números imaginarios
8.2.2 Raíces complejas
8.2.3 Más números complejos y ecuaciones
Sección 8.3
8.3.1 División de polinomios
8.3.2 Factores y raíces enteras
8.3.3 Una aplicación de polinomios
Resumen del Capítulo
Sección 9.1
9.1.1 Diseño de encuestas
9.1.2 Muestras y el rol de la aleatorización
9.1.3 Sesgo en muestras por conveniencia
Sección 9.2
9.2.1 Probando la causa y el efecto con experimentos
9.2.2 Conclusiones a partir de estudios
Sección 9.3
9.3.1 Histogramas de frecuencia relativa
9.3.2 La función de densidad de probabilidad normal
9.3.3 Percentiles
Resumen del Capítulo
Sección 10.1
10.1.1 Introducción a las series aritméticas
10.1.2 Más series aritméticas
10.1.3 Series aritméticas generales
10.1.4 Notación de suma y combinaciones de series
Sección10.2
10.2.1 Series geométricas
10.2.2 Series infinitas
Sección10.3
10.3.1 El triángulo de Pascal y el Teorema del binomio
10.3.2 El númeroe
Resumen del Capítulo
Sección 11.1
11.1.1 Simulaciones de probabilidad
11.1.2 Más simulaciones de probabilidad
11.1.3 Simulación de la variabilidad muestral
Sección 11.2
11.2.1 Evaluación estadística usando la variabilidad muestral
11.2.2 Variabilidad en los resultados experimentales
11.2.3 Control de calidad
11.2.4 Control estadístico de procesos
Sección 11.3
11.3.1 Análisis de decisiones y estrategias
Resumen del Capítulo
Sección 12.1
12.1.1 Analizando ecuaciones trigonométricas
12.1.2 Soluciones de las ecuaciones trigonométricas
12.1.3 Inversas de las funciones trigonométricas
12.1.4 Funciones trigonométrica recíprocas
Sección 12.2 12.2.1 Identidades trigonométricas
12.2.2 Demostrando identidades trigonométricas
12.2.3 Identidades de suma y diferencia de ángulos
Resumen del Capítulo
Sección A.1
A.1.1 Representación del crecimiento exponencia
A.1.2 Razones de rebote
A.1.3 El balón que rebota y el decaimiento exponencial
Sección A.2
A.2.1 Generación e investigación de progresiones
A.2.2 Generalización de progresiones aritméticas
A.2.3 Progresiones recurrentes
SecciónA.3
A.3.1 Patrones de crecimiento en tablas y gráficos
A.3.2 Uso de multiplicadores para resolver problemas
‘A.3.3 Comparación de progresiones y funciones
Resumen del Apéndice
Sección B.1
B.1.1 Investigar y= bx
B.1.2 Múltiples representaciones de funciones exponenciales
B.1.3 Más aplicaciones del crecimiento exponencial
B.1.4 Decaimiento exponencial
B.1.5 Gráfico →ecuación
B.1.6 Completar la red de representaciones múltiples
Sección B.2
B.2.1 Curvas de ajuste y exponentes fraccionariosB31B.2.2Más curvas de ajuste
B.2.3 Resolución gráfica de un sistema de funciones exponenciales
Resumen del Apéndice
Sección C.1
C.1.1 Investigación de representaciones de datos
C.1.2 Comparación de datos
C.1.3 Desviación estándar
Section 1.1
1.1.1 Solving Puzzles in Teams
1.1.2
Investigating the Growth of Patterns
1.1.3 Investigating the Graphs of Quadratic Functions
Section 1.2
1.2.1 Describing a
Graph
1.2.2 Cube Root and Absolute Value Functions
1.2.3 Function Machines
1.2.4 Functions
1.2.5 Domain and Range
Chapter Closure
Section 2.1
2.1.1 Seeing Growth in Linear Representations
2.1.2 Slope
2.1.3 Comparing Δy and Δx
2.1.4 y = mx + b and More on Slope
Section 2.2
2.2.1 Slope as Motion
2.2.2 Rate of Change
2.2.3 Equations of Lines in Situations
Section 2.3
2.3.1 Finding an Equation Given a Slope and a Point
2.3.2 Finding the Equation of a Line Through Two Points
Extension Activity Finding y = mx + b from Graphs and Tables
Chapter Closure
Section 3.1
3.1.1 Simplifying Exponential Expressions
3.1.2 Zero and Negative Exponents
Section 3.2
3.2.1 EquationsAlgebra Tiles
3.2.2 Exploring an Area Model
3.2.3 Multiplying Binomials and the Distributive Property
3.2.4 Using Generic Rectangles to Multiply
Section 3.3
3.3.1 Solving Equations With Multiplication and Absolute Value
3.3.2 Working With Multi-Variable Equations
3.3.3 Summary of Solving Equations
Chapter Closure
Section 4.1
4.1.1 Solving Word Problems by Writing Equations
4.1.2 One Equation or Two?
Section 4.2
4.2.1 Solving Systems of Equations Using Substitution
4.2.2 Making Connections: Systems, Solutions, and Graphs
4.2.3 Solving Systems Using Elimination
4.2.4 More Elimination
4.2.5 Choosing a Strategy for Solving Systems
Section 4.3
4.3.1 Pulling it all Together
Chapter Closure
Section 6.1
6.1.1 Line of Best Fit
6.1.2 Residuals
6.1.3 Upper and Lower Bounds
6.1.4 Least Squares Regression Line
Section 6.2
6.2.1 Residual Plots
6.2.2 Correlation
6.2.3 Association is N
ot Causation
6.2.4 Interpreting Correlation in Context
6.2.5 Curved Best – Fit
Models
Chapter Closure
| Opening | 6.OP | Chapter Opening |
|---|---|---|
| Section 6.1 | 6.1.1 | Dividing |
| 6.1.2 | Fractions as Division Problems | |
| 6.1.3 | Problem Solving with Division | |
| 6.1.4 | Solving Problems Involving Fraction Division | |
| Section 6.2 | 6.2.1 | Order of Operations |
| 6.2.2 | Area of a Rectangular Shape | |
| 6.2.3 | Naming Perimeters of Algebra Tiles | |
| 6.2.4 | Combining Like Terms | |
| 6.2.5 | Evaluating Algebraic Expressions | |
| Closure | 6.CL | Chapter Closure |
Section 7.1
7.1.1 Investigating y= bx^3
7.1.2 Multiple Representations of Exponential Functions
7.1.3 More Applications of Exponential Growth
7.1.4 Exponential Decay
7.1.5 Graph→Equation
7.1.6 Completing the Multiple Representations Web
Section 7.2
7.2.1 Curve Fitting and Fractional Exponents
7.2.2 More Curve Fitting
7.2.3 Solving a System of Exponential Functions Graphically
Chapter Closure
Section 8.1
8.1.1 Introduction to Factoring Quadratics
8.1.2 Factoring with Generic Rectangles
8.1.3 Factoring with Special Cases
8.1.4 Factoring Completely
8.1.5 Factoring Shortcuts
Section 8.2
8.2.1 Multiple Representations for Quadratic Functions
8.2.2 Zero Product Property
8.2.3 More Ways To Find the x-Intercepts
8.2.4 Completing the Quadratic Web
8.2.5 Completing the Square
Chapter Closure
Section 9.1
9.1.1 Solving Quadratic Equations
9.1.2 Introduction to the Quadratic Formula
9.1.3 More Solving Quadratic Equations
9.1.4 Choosing a Strategy
Section 9.2
9.2.1 Solving Linear, One-Variable Inequalities
9.2.2 More Solving Inequalities
Section 9.3
9.3.1 Graphing Two-Variable Inequalities
9.3.2 Graphing Linear and Non-Linear Inequalities
Section 9.4
9.4.1 Systems of Inequalities
9.4.2 More Systems of Inequalities
9.4.3 Applying Inequalities to Solve Problems
Chapter Closure
Section 10.1
10.1.1 Association in Two-Way Tables
Section 10.2
10.2.1 Solving by Rewriting
10.2.2 Fraction Busters
10.2.3 Multiple Methods for Solving Equations
10.2.4 Determining the Number of Solutions
10.2.5 Deriving the Quadratic Formula and the Number System
10.2.6 More Solving and an Application
Section 10.3
10.3.1 Intersection of Two Functions
10.3.2 Number of Parabola Intersections
10.3.3 Solving Quadratic and Absolute Value Inequalities
Chapter Closure
Section 11.1
11.1.1 Transforming Functions
11.1.2 Inverse Functions
Section 11.2
11.2.1 Investigating Data Representations
11.2.2 Comparing Data’
11.2.3 Standard Deviation
Section 11.3
11.3.1 Using a Best-Fit Line to Make a Prediction
11.3.2 Relation Treasure Hunt
11.3.3 Investigating a Complex Function
11.3.4 Using Algebra to Find a Maximum
11.3.5 Exponential Functions and Linear Inequalities
Chapter Closure
Section A.1
A.1.1 Exploring Variables and Combining Like Terms
A.1.2 Simplifying Expressions by Combining Like Terms
A.1.3 Writing Algebraic Expressions
A.1.4 Using Zero to Simplify Algebraic Expressions
A.1.5 Using Algebra Tiles to Simplify Algebraic Expressions
A.1.6 Using Algebra Tiles to Compare Expressions
A.1.7 Simplifying and Recording Work
A.1.8 Using Algebra Tiles to Solve for x
A.1.9 More Solving Equations
Chapter Closure
Section 1.1
1.1.1 Creating Quilt Using Symmetry
1.1.2 Making Predictions and Investigating Results
1.1.3 Perimeters and Areas of Enlarging Tile Patterns
1.1.4 Logical Arguments
1.1.5 Building a Kaleidoscope
Section 1.2
1.2.1 Spatial Visualization and Reflection
1.2.2 Rigid Transformations: Rotation and Translations
1.2.3 Slope of Parallel and Perpendicular Lines
1.2.4 Defining Transformations
1.2.5 Using Transformations to Create Shapes
1.2.6 Symmetry
Section 1.3
1.3.1 Attributes and Characteristics of Shapes
1.3.2 More Characteristics of Shapes
Chapter Closure
Section 2.1
2.1.1 Complementary, Supplementary, and Vertical Angles
2.1.2 Angles Formed by Transversals
2.1.3 More Angles Formed by Transversals
2.1.4 Angles in a Triangle
2.1.5 Applying Angle Relationships
Section 2.2
2.2.1 Units of Measure
2.2.2 Areas of Triangles and Composite Shapes
2.2.3 Areas of Parallelograms and Trapezoids
2.2.4 Heights and Areas
Section 2.3
2.3.1 Triangle Inequality
2.3.2 The Pythagorean Theorem
Chapter Closure
Section 3.1
3.1.1 Dilations
3.1.2 Similarity
3.1.3 Using Ratios of Similarity
3.1.4 Applications and Notation
Section 3.2
3.2.1 Conditions for Triangle Similarity
3.2.2 Creating a Flowchart
3.2.3 Triangle Similarity and Congruence
3.2.4 More Conditions for TriangleSimilarity
3.2.5 Determining Similarity
3.2.6 Applying Similarity
Chapter Closure
Section 4.1
4.1.1 Constant Ratios in Right Triangles
4.1.2 Connecting Slope Ratios to Specific Angles
4.1.3 Expanding the Trig Table
4.1.4 The Tangent Ratio
4.1.5 Applying the Tangent Ratio
Section 4.2
4.2.1 Using an Area Model
4.2.2 Using a Tree Diagram
4.2.3 Probability Models
4.2.4 Unions, Intersections, and Complements
4.2.5 Expected Value
Chapter Closure
Section 5.1
5.1.1 Sine and Cosine Ratios
5.1.2 Selecting a Trig Tool
5.1.3 Inverse Trigonometry
5.1.4 Applications
Section 5.2
5.2.1 Special Right Triangles
5.2.2 Pythagorean Triples
Section 5.3
5.3.1 Finding Missing Parts of Triangles
5.3.2 Law of Sines
5.3.3 Law of Cosines
5.3.4 Ambiguous Triangles(Optional)
5.3.5 Choosing a Tool
Chapter Closure
Section 6.1
6.1.1 Congruent Triangles3
6.1.2 Conditions for Triangle Congruence
6.1.3 Congruence of Triangles Through Rigid Transformations3526.1.4Flowcharts for Congruence
6.1.5 Converses
Section 6.2
6.2.1 Angles on a Pool Table
6.2.2 Investigating a Triangle
6.2.3 Creating a Mathematical Model
6.2.4 Analyzing a Game’
6.2.5 Using Transformations and Symmetry to Design Snowflakes
Chapter Closure
Section 7.1
7.1.1 Properties of a Circle
7.1.2 Building a Tetrahedron
7.1.3 Shortest Distance Problems
7.1.4 Using Symmetry to Study Polygons
Section 7.2
7.2.1 Special Quadrilaterals and Proof
7.2.2 Properties of Rhombi
7.2.3 More Proofswith Congruent Triangles
7.2.4 MoreProperties of Quadrilaterals
7.2.5 Two-Column Proofs
7.2.6 Explore-Conjecture-Prove
Section 7.3
7.3.1 Studying Quadrilaterals on a Coordinate Grid
7.3.2 Coordinate Geometry and Midpoints
7.3.3 Identifying Quadrilaterals on a Coordinate Grid
Chapter Closure
Section 8.1
8.1.1 Pinwheels and Polygons
8.1.2 Interior Angles of Polygons
8.1.3 Angles of Regular Polygons
8.1.4 Regular Polygon Angle Connections
8.1.5 Finding Areas of Regular Polygons
Section 8.2
8.2.1 Area Ratios of Similar Figures
8.2.2 Ratios of Similarity
Section 8.3
8.3.1 A Special Ratio
8.3.2 Area and Circumference of a Circle
8.3.3 Circles in Context
Chapter Closure
Section 9.1
9.1.1 Three-Dimensional Solids
9.1.2 Volumesand Surface Areas of Prisms
9.1.3 Prisms and Cylinders
9.1.4 Volumes of Similar Solids
9.1.5 Ratios of Similarity
Section 9.2
9.2.1 Introduction to Constructions
9.2.2 Constructing Bisectors
9.2.3 More Explorations with Constructions
9.2.4 Other Constructions
Chapter Closure
Section 10.1
10.1.1 Introduction to Chords
10.1.2 Angles and Arcs
10.1.3 Chords and Angles
10.1.4 Tangents and Secants
10.1.5 Problem Solving with Circles
Section 10.2
10.2.1 Conditional Probability and Independence
10.2.2 Two-Way Tables
10.2.3 Applications of Probability
Section 10.3
10.3.1 The Fundamental Principle of Counting
10.3.2 Permutations
10.3.3 Combinations
10.3.4 Categorizing Counting Problems
10.3.5 Some Challenging Probability Problems
Chapter Closure
Section 11.1
11.1.1 Platonic Solids
11.1.2 Pyramids
11.1.3 Volume of a Pyramid
11.1.4 Surface Area and Volume of a Cone
11.1.5 Surface Area and Volume of a Sphere
Section 11.2
11.2.1 Coordinates on a Sphere
11.2.2 Tangents and Arcs
11.2.3 Secant and Tangent Relationships
Chapter Closure
Section 12.1
12.1.1 The Equation of a Circle
12.1.2 Completing the Square for Equations of Circles
12.1.3 Introduction to Conic Sections
12.1.4 Graphing a ParabolaUsing the Focus and Directrix
Section 12.2
12.2.1 Using Coordinate Geometry and Constructions to Explore Shapes
12.2.2 Euler’s Formula for Polyhedra
12.2.3 The Golden Ratio
12.2.4 Using Geometry to find Probabilities
Chapter Closure
Section 1.1
1.1.1 Solving Puzzles in Teams
1.1.2 Using a Graphing Calculator to Explore a Function
1.1.3 Domain and Range
1.1.4 Points of Intersection in Multiple Representations
Section 1.2
1.2.1 Modeling a Geometric Relationship
1.2.2 Function Investigation
1.2.3 The Family of Linear Functions
1.2.4 Function Investigation Challenge
Chapter Closure
Section 2.1
2.1.1 Modeling Non-Linear Data
2.1.2 Parabola Investigation
2.1.3 Graphing a Parabola Without a Table
2.1.4 Rewriting in Graphing Form
2.1.5 Mathematical Modeling with Parabolas
Section 2.2
2.2.1 Transforming Other Parent Graphs
2.2.2 Describing (h,k) for Each Family of Functions
2.2.3 Transformations of Functions
2.2.4 Transforming Non-Functions
2.2.5 Transforming Piecewise-Defined Functions
Chapter Closur
Section 3.1
3.1.1 Equivalent Expressions
3.1.2 Rewriting Expressions and Determining Equivalence
3.1.3 Solving by Rewriting
Section 3.2
3.2.1 Investigating Rational Functions
3.2.2 Simplifying Rational Expressions
3.2.3 Multiplying and Dividing Rational Expressions
3.2.4 Adding and Subtracting Rational Expressions
3.2.5 Creating New Functions
Chapter Closure
Section 4.1
4.1.1 Strategies for Solving Equations
4.1.2 Solving Equations and Systems Graphically
4.1.3 Finding Multiple Solutions to Systems of Equations
4.1.4 Using Systems of Equations to Solve Problems
Section 4.2
4.2.1 Solving Inequalities with One or Two Variables
4.2.2 Using Systems to Solve a Problem
4.2.3 Application of Systems of Linear Inequalities
4.2.4 Using Graphs to Find Solutions
Chapter Closure
Section 5.1
5.1.1 “Undo” Equations
5.1.2 Using a Graph to Find an Inverse
5.1.3 Finding Inverses and Justifying Algebraically
Section 5.2
5.2.1 Finding the Inverse of an Exponential Function
5.2.2 Defining the Inverse of an Exponential Function
5.2.3 Investigating the Family of Logarithmic Functions
5.2.4 Transformations of Logarithmic Functions
5.2.5 Investigating Compositions of Functions
Chapter Closure
Section 6.1
6.1.1 Creating a Three-Dimensional Model
6.1.2 Graphing Equations in Three Dimensions
6.1.3 Systems of Three-Variable Equations2666.1.4Solving Systems of Three Equations with Three Unknowns
6.1.5 Using Systems of Three Equations for Curve Fitting
Section 6.2
6.2.1 Using Logarithms to Solve Exponential Equations
6.2.2 Investigating the Properties of Logarithms
6.2.3 Writing Equations of Exponential Functions
6.2.4 An Application of Logarithms
Chapter Closure
Section 7.1
7.1.1 Introduction to Cyclic Models
7.1.2 Graphing the Sine Function
7.1.3 Unit Circle ↔Graph
7.1.4 Graphing and Interpreting the Cosine Function
7.1.5 Defining a Radian
7.1.6 Building a Unit Circle
7.1.7 The Tangent Function
Section 7.2 7.2.1 Transformations of y= sin x
7.2.2 One More Parameter for a Cyclic Function
7.2.3 Period of a Cyclic Function
7.2.4 Graph ↔Equation
Chapter Closure
Section 8.1
8.1.1 Sketching Graphs of Polynomial Functions
8.1.2 More Graphs of Polynomials
8.1.3 Stretch Factorsfor Polynomial Functions
Section 8.2
8.2.1 Introducing Imaginary Numbers
8.2.2 Complex Roots
8.2.3 More Complex Numbers and Equations
Section 8.3
8.3.1 Polynomial Division
8.3.2 Factors and Integral Roots
8.3.3 An Application of Polynomials
Chapter Closure
Section 9.1
9.1.1 Survey Design4
9.1.2 Samples and the Role of Randomness
9.1.3 Bias in Convenience Samples
Section 9.2
9.2.1 Testing Causeand Effect with Experiments
9.2.2 Conclusions From Studies
Section 9.3
9.3.1 Relative Frequency Histograms
9.3.2 The Normal Probability Density Function
9.3.3 Percentiles
Chapter Closure
Section 10.1
10.1.1 Introduction to Arithmetic Series
10.1.2 More Arithmetic Series
10.1.3 General Arithmetic Series
10.1.4 Summation Notation and Combinations of Series
Section 10.2
10.2.1 Geometric Series
10.2.2 Infinite Series
Section 10.3
10.3.1 Pascal’s Triangle and the Binomial Theorem
10.3.2 TheNumber e
Chapter Closure
Section 11.1
11.1.1 Simulations of Probability
11.1.2 More Simulations of Probability
11.1.3 Simulating Sampling Variability
Section 11.2
11.2.1 Statistical Test Using Sampling Variability
11.2.2 Variability in Experimental Results
11.2.3 Quality Control
11.2.4 Statistical Process Control
Section11.3
11.3.1 Analyzing Decisions and Strategies
Chapter Closure
Section 12.1
12.1.1 Analyzing Trigonometric Equations
12.1.2 Solutions to Trigonometric Equations
12.1.3 Inverses of Trigonometric Functions
12.1.4 Reciprocal Trigonometric Functions
Section 12.2
12.2.1 Trigonometric Identities
12.2.2 Proving Trigonometric Identities
12.2.3 Angle Sum and Difference Identities
Chapter Closure
Section A.1
A.1.1 Representing Exponential Growth
A.1.2 Rebound Ratios
A.1.3 The Bouncing Ball and Exponential Decay
Section A.2
A.2.1 Generating and Investigating Sequences
A.2.2 Generalizing Arithmetic Sequences
A.2.3 Recursive Sequences
Section A.3
A.3.1 Patterns of Growth in Tables and Graphs
A.3.2 Using Multipliers to Solve Problems
A.3.3 Comparing Sequences to Functions
Appendix Closure
Section B.1
B.1.1 Investigation y = bx
B.1.2 Multiple Representations of Exponential Functions
B.1.3 More Applications of Exponential Growth
B.1.4 Exponential Decay
B.1.5 Graph → Equation
B.1.6 Completing the Multiple Representations Web
Section B.2
B.2.1 Curve Fitting and Fractional Exponents
B.2.2 More Curve Fitting
B.2.3 Solving a System of Exponential Functions Graphically
Appendix Closure
Section C.1
C.1.1 Investigating Data Representations
C.1.2 Comparing Data
C.1.3 Standard Deviation
Appendix Closure
CP 1: Using Place Value to Round and Compare Decimals
CP 2: Addition and Subtraction of Decimals
CP 3: Addition and Subtraction of Fractions
CP 4: Addition and Subtraction of Mixed Numbers
CP 5: Multiple Representations of Portions
P 6: Locating Points on a Number Line and on a Coordinate Graph
CP 7A: Multiplication of Fractions and Decimals
CP 7B: Area and Perimeter of Quadrilaterals and Triangles
CP 8A: Rewriting and Evaluating Variable Expressions
CP 8B: Division of Fractions and Decimals
CP 9A: Displays of Data: Histograms and Box Plots
CP 9B: Solving One-Step Equations
Section 6.1
6.1.1 Comparing Expressions
6.1.2 Comparing Quantities with Variables
6.1.3 One Variable Inequalities
6.1.4 Solving One Variable Inequalities
Section 6.2
6.2.1 Solving Equations
6.2.2 Checking Solutions and the Distributive Property
6.2.3 Solving Equations and Recording Work
6.2.4 Using a Table to Write Equations from Word Problems
6.2.5 Writing and Solving Equations
6.2.6 Cases with Infinite or No Solutions
6.2.7 Choosing a Solving Strategy
Chapter Closure
Section 7.1
7.1.1 Distance, Rate, and Time
7.1.2 Scaling Quantities
7.1.3 Solving Problems Involving Percents
7.1.4 Equations with Fraction and Decimal Coefficients
7.1.5 Creating Integer Coefficients
7.1.6 Creating Integer Coefficients Efficiently
7.1.7 Percent Increase and Decrease
7.1.8 Simple Interest
Section 7.2
7.2.1 Finding Missing Information in Proportional Relationships
7.2.2 Solving Proportions
Chapter Closure
Section 8.1
8.1.1 Measurement Precision
8.1.2 Comparing Distributions
Section 8.2
8.2.1 Representative Samples
8.2.2 Inference from Random Samples
Section 8.3
8.3.1 Introduction to Angles
8.3.2 Classifying Angles
8.3.3 Constructing Shapes
8.3.4 Building Triangles
Chapter Closure
Section 9.1
9.1.1 Circumference, Diameter, and Pi
9.1.2 Area of Circles
9.1.3 Area of Composite Shapes
Section 9.2
9.2.1 Surface Area and Volume
9.2.2 Cross Sections
9.2.3 Volume of a Prism
9.2.4 Volume of Non-Rectangular Prisms
Chapter Closure
Section 9.3
9.3.1 Volume and Scaling
9.3.2 Using Multiple Math Ideas to Create an Interior Design
9.3.3 Applying Ratios
Checkpoint 1: Area and Perimeter of Polygons
Checkpoint 2: Multiple Representations of Portions
Checkpoint 3: Multiplying Fractions and Decimals
Checkpoint 5: Order of Operations
Checkpoint 6: Writing and Evaluating Algebraic Expressions
Checkpoint 7A: Simplifying Expressions
Checkpoint 7B: Displays of Data: Histograms and Box Plots
Checkpoint 8: Solving Multi-Step Equations
Checkpoint 9: Unit Rates and Proportions
Section 6.1
6.1.1 Rigid Transformations
6.1.2 Rigid Transformations on a Coordinate Graph
6.1.3 Describing Transformations
6.1.4 Using Rigid Transformations
Section 6.2
6.2.1 Multiplication and Dilation
6.2.2 Dilations and Similar Figures
6.2.3 Identifying Similar Shapes
6.2.4 Similar Figures and Transformations
6.2.5 Working With Corresponding Sides
6.2.6 Solving Problems Involving Similar Shapes
Chapter Closure
Section 7.1
7.1.1 Circle Graphs
7.1.2 Organizing Data in a Scatterplot
7.1.3 Identifying and Describing Association
Section 7.2
7.2.1 y = mx + b Revisited
7.2.2 Slope
7.2.3 Slope in Different Representations
7.2.4 More About Slope
7.2.5 Proportional Equations
Section 7.3
7.3.1 Using Equations to Make Predictions
7.3.2 Describing Association Fully
7.3.3 Association Between Categorical Variables
Chapter Closure
Section 8.1
8.1.1 Patterns of Growth in Tables and Graphs
8.1.2 Compound Interest
8.1.3 Linear and Exponential Growth
Section 8.2
8.2.1 Exponents and Scientific Notation
8.2.2 Exponent Rules
8.2.3 Negative Exponents
8.2.4 Operations with Scientific Notation
Section 8.3
8.3.1 Functions in Graphs and Tables
Chapter Closure
Section 9.1
9.1.1 Parallel Line Angle Pair Relationships
9.1.2 Finding Unknown Angles in Triangles
9.1.3 Exterior Angles in Triangles
9.1.4 AA Triangle Similarity
Section 9.2
9.2.1 Side Lengths and Triangles
9.2.2 Pythagorean Theorem
9.2.3 Understanding Square Root
9.2.4 Real Numbers
9.2.5 Applications of the Pythagorean Theorem
9.2.6 Pythagorean Theorem in Three Dimensions
9.2.7 Pythagorean Theorem Proofs
Chapter Closure
Section 10.1
10.1.1 Cube Roots
10.1.2 Surface Area and Volume of a Cylinder
10.1.3 Volumes of Cones and Pyramids
10.1.4 Volume of a Sphere
10.1.5 Applications of Volume
Chapter Closure
10.2.1 Indirect Measurement
10.2.2 Finding Unknowns
10.2.3 Analyzing Data to Identify a Trend
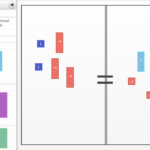
1. Operations with Signed Fractions and Decimals
2. Evaluating Expressions and Using Order of Operations
3. Unit Rates and Proportions
4. Area and Perimeter of Circles and Composite Figures
5. Solving Equations
6. Multiple Representations of Linear Equations
7. Solving Equations with Fractions and Decimals (Fraction Busters)
8. Transformations
9. Scatterplots and Association
0.1.1
Who are my classmates?
0.1.2
How do I work collaboratively?
0.1.3
What questions can I ask?
0.1.4
How can I categorize my words?
0.1.5
How can I communicate my ideas?
0.1.6
How can the team build this together?
0.1.7
What do we need to work togethe
1.1 Numbers and Data
1.1.1 How should data be placed on this line?
1.1.2 Where do these numbers belong on this line?
1.1.3 How can I use two lines to solve problems?
1.1.4 How can data be used to answer a question?
1.1.5 How are histograms helpful?
1.1.6 How else can data be displayed?
1.2 Shapes and Area,
1.2.1 How can I write equivalent expressions in area and perimeter?
1.2.2 What shapes make up the polygon?
1.2.3 How can I make it a rectangle?
1.3 Expressions
1.3.1 How can I describe it using symbols?
1.3.2 What are the parts of an expression?
1.3.3 How do I work with decimals?
1.3.4 How do I multiply multi-digit decimals?
1.3.5 How can I represent the arrangement?
2.1 Ratio Language
2.1.1 How can I compare two quantities?
2.1.2 How can I write ratios?
2.1.3 How can I see ratios in data representations?
2.2 Equivalent Ratios
2.2.1 How can I visualize ratios?
2.2.2 How can I see equivalent ratios in a table?
2.2.3 How can I see equivalent ratios in a double number line?
2.2.4 How can I see equivalent ratios in tape diagrams?
2.2.5 How can I use equivalent ratios?
2.2.6 What do these represent?
2.3 Measurement
2.3.1 What are the measurements?
2.3.2 What are the units?
2.3.3 How can I convert units
3.1 Measures of Center
3.1.1 How can I measure the center?
3.1.2 How else can I measure the center?
3.1.3 Which is the better measure of center?
3.1.4 What happens when I change the data?
3.2 Integers
3.2.1 What numbers do I see?
3.2.2 What number is this?
3.2.3 What does a number line say about a number?
3.2.4 How do I compare different types of numbers?
3.3 Absolute Value
3.3.1 How do I describe the location?
3.3.2 How far do I walk?
3.3.3 Which one is greater?
3.3.4 How do I communicate mathematically?
3.4 Coordinate Plane
3.4.1 How can you precisely indicate a location?
3.4.2 What is the correct order?
3.4.3bWhat symbol represents me?
4.1 Fractions, Decimals, and Percents
4.1.1 How can I tell if the ratios are equal?
4.1.2 What does “percent” mean?
4.1.3 How can I convert a fraction?
4.1.4 How can I convert a percent?
4.1.5 How can I convert a decimal?
5.1 Variation in Data
5.1.1 How do I ask a statistical question?
5.1.2 What does each representation say about the data?
5.1.3 What does the box in a box plot represent?
5.1.4 How else can I describe data?
5.2 Area
5.2.1 What is the height?
5.2.2 Can I reconfigure a parallelogram into a rectangle?
5.2.3 How do I calculate the area?
5.2.4 How many triangles do I need?
5.2.5 What is my perspective?
5.2.6 Is it fair to play by the rules?
5.2.7 What shapes do I see?
5.3 Fractions
5.3.1 How can I represent fraction multiplication?
5.3.2 How can I multiply fractions?
5.3.3 How can I multiply mixed numbers?
6.1 Rules of Operations
6.1.1 What does it mean?
6.1.2 What do mathematicians call this?
6.1.3 How much should I ask for?
6.1.4 How can I write mathematical expressions?
6.1.5 How do mathematicians abbreviate?
6.1.6 In what order should I evaluate?
6.2 Multiples and Factors
6.2.1 When will they be the same?
6.2.2 What are multiples?
6.2.3 What do they have in common?
6.2.4 Who is your secret valentine?
6.2.5 How can I understand products?
6.2.6 How can I rewrite expressions?
6.2.7 Which method do I use?
7.1 Whole Number and Decimal Division
7.1.1 How can I share equally?
7.1.2 Which strategy is the most efficient?
7.1.3 How can I write the number sentence?
7.1.4 How can I divide decimals?
7.1.5 How should the problem be arranged?
7.2 Fraction Division
7.2.1 What if the divisor is a fraction?
7.2.2 How many fit?
7.2.3 How can I visualize this?
7.2.4 What is common about this?
7.2.5 How can I use a Giant One?
7.2.6 Which method is most efficient?
8.1. Algebra Tiles
8.1.1 What do these shapes represent?
8.1.2 What does a group of tiles represent?
8.1.3 What is an equivalent expression?
8.1.4 Which terms can be combined?
8.1.5 What do the numbers mean?
8.1.6 What can a variable represent?
8.2 Expressions
8.2.1 How can I count it?
8.2.2 What if the size of the pool is unknown?
8.2.3 How can I use an algebraic expression?
8.3 Equations and Inequalities
8.3.1 Which values make the equation true?
8.3.2 How can patterns be represented?
8.3.3 What is the equation?
8.3.4 How many could there be?
0.1.1 What do they have in common?
0.1.2 How can I effectively communicate with my team?
0.1.3 Is there another perspective?
0.1.4 How can I persevere through struggle?
0.1.5 How can I see this happening?
0.1.6 What patterns can I recognize?
0.1.7 What is the best strategy?
0.1.8 How does respect look?
1.1 Data and Graphs
1.1.1 How can I represent data?
1.1.2 How can I use data to solve a problem?
1.1.3 Is the roller coaster safe?
1.1.4 Is there a relationship?
1.1.5 What is the relationship?

This professional learning is designed for teachers as they begin their implementation of CPM. This series contains multiple components and is grounded in multiple active experiences delivered over the first year. This learning experience will encourage teachers to adjust their instructional practices, expand their content knowledge, and challenge their beliefs about teaching and learning. Teachers and leaders will gain first-hand experience with CPM with emphasis on what they will be teaching. Throughout this series educators will experience the mathematics, consider instructional practices, and learn about the classroom environment necessary for a successful implementation of CPM curriculum resources.
Page 2 of the Professional Learning Progression (PDF) describes all of the components of this learning event and the additional support available. Teachers new to a course, but have previously attended Foundations for Implementation, can choose to engage in the course Content Modules in the Professional Learning Portal rather than attending the entire series of learning events again.