These high-quality middle school math programs prepare 6th, 7th, and 8th grade students with powerful mathematical thinking and problem-solving skills.
Includes two unique middle school programs and a support class:

• Meaningful Mathematics
• Multimodal program utilizing both digital & print materials
• Dynamic teacher-guided pacing technology
• Intentional mix of digital, print, and manipulatives
• Consumable student book called the Mathematician’s Notebook

• CPM’s time-tested program
• Based on research & CPM’s Three Pillars
• Option of digital and/or print materials
• English and Spanish

What does a full blend of print and digital look like? In this multimodal series, digital and print materials work in tandem to maximize student engagement. The choice of medium for each aspect of a lesson is based on how and where students learn best.

Students have a personal notebook to record the messy work of learning. Here, they highlight key concepts, questions, rough draft thinking, mistakes, corrections, and their inspirations. The Mathematician’s Notebook provides diagrams and graphs for students to work with, and plenty of space so that students have room for error and experimentation.
Concise goals for each lesson are presented to the teacher and to students in the chapter introductions, referenced in the Reflection & Practice problems, and revisited in Chapter Closures. The Mathematician’s Notebook contains a printed copy of the Learning Targets where students can keep track of their progress throughout the course.

Problems are designed to facilitate student learning per the learning intent. To maximize student sensemaking and engagement, lessons have been intentionally constructed using a variety of venues for student work.

Inspiring Connections guides teachers through lessons.
The authors describe how they envision the lesson progressing. These notes are summarized into brief descriptions, which can serve as a reminder after reading the full Authors’ Vision.
The Lesson at a Glance provides a quick orientation to the lesson. It lists things to consider as you prepare to teach the lesson: the overview, learning intent, materials needed, aligning standards, and additional resources.

Lessons are designed for students to work in teams during a 45-minute period.

Students collaborate in teams for the large majority of class time. As a means to help all students have a voice and be an integral part of their team, four roles are presented in the Prelude and referred to throughout the curriculum. The roles are Representative, Coordinator, Organizer, and Investigator.
A variety of Study Team and Teaching Strategies (STTS) are suggested in the Authors’ Vision throughout Inspiring Connections. These strategies may be used to help structure team interactions and facilitate engagement. As you gain experience with the curriculum and get to know your students, you will likely develop your own favorite strategies to use regularly.






Inspirations & Ideas is a compilation of lessons, arranged appropriately in units, that convey multiple objectives. Although each unit may not fully address a single objective, as a compilation, the objectives are met. The course does not attempt to address every content standard in the 8th grade curriculum. Rather, the math content in the course is used as a vehicle to change students’ beliefs and attitudes about math. Inspirations & Ideas focuses on the following themes:
Incorrect ideas are often necessary to develop correct ideas.
• Honoring mistakes
• Trial and error/Guess and Check
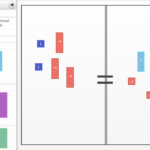
Mathematics is visual.
• Multiple representations
• Patterns
Effective communication in mathematics should be practiced.
• Giving and receiving effective math feedback
• Justifying mathematics verbally and in writing
Problem-solving strategies make problems accessible.
• Working backwards
• Making the problem smaller
• Organizing information
Building relationships is vital to a positive classroom environment.
* Individual progress checks with the teacher
• Student reflection journals
• Goal setting
Students can re-engage with mathematics in new ways.
• Ratio
• Proportion
• Equivalence
• Solving
• Numeracy
• Patterns
• Graphing
• Fractions
• Exponents

© 1989-2025 CPM EDUCATIONAL PROGRAM All rights reserved. CPM Educational Program is a 501(c)(3) educational nonprofit corporation.