Have you ever facilitated a number talk in your classroom only to have the same five students share their strategies? Because the purpose of number talks is to increase number sense, recognize patterns, and reach higher-level mathematical discourse, we have utilized different strategies to help provide more risk-free ways for all students to participate. These strategies (Guest Recorder, Can You Make it?, Team Number Talk, Which One Doesn’t Belong?) give students a chance to discuss their thinking in small groups. This in turn helps students build confidence in sharing and conversing with a larger group. We also realized that we had to ensure that the problems we presented to the students allowed for a variety of ways to arrive at a solution. Below are descriptions of these different strategies.
Which One Doesn’t Belong?
Megan Mastrocola, Hartland, WI meganmastrocola@cpm.org
Another type of number talk that has been successful is a Which One Doesn’t Belong? Number Talk. This type of number talk definitely helps increase participation. The purpose of this type of number talk is for students to look at four different representations and pick the one that they think does not belong.The best part about this is that there is no wrong answer! This helps make the problem accessible for all students. The goal is for the team to justify their reasons as strongly and as clearly as they can, supporting the statements they make. The procedure is the same as a number talk: Holding their fist to their chests, students will put up their thumb when they have decided which one does not belong, and then each finger represents the reason(s) they have. After that, the students share their reasons with their team. The team decides which item they want to support and one person records their reasons. Each team selects a student to share their team’s decision. During this sharing time, we talk about how to be more clear and complete. I then choose the team that was able to make the clearest and most complete argument for their choice. The students really get motivated to make the most sound mathematical justifications. They work hard at coming up with irrefutable reasons using many vocabulary words. In class, our conversations have shifted as we learn more throughout the year. Now, students say “My strategy is similar to …”, “I want to clarify my answer because…”, “I want to challenge this team’s thinking and this is how…” or “I hear what you are saying, but another way could be…” The students have shared that they really enjoy doing this type of number talk because all students can be involved and share their solutions. Which One Doesn’t Belong? allows students to talk more about the reasons rather than just solving an equation. Luckily, there are plenty of resources for this type of number talk, both online and in the book by Christopher Danielson. Many examples can be found at Which One Doesn’t Belong?
Guest Recorder
Dan Chandler, De Pere, WI danchandler@cpm.org
I conduct number talks once a week in my four sections of Core Connections, Algebra 2. In these number talks I have observed many student outcomes and behaviors that show up consistently, no matter which concept the talk is covering. Some of these include: students that develop a method of solution in real time as they explain an answer, students that help each other with their solution, and students that find errors in their reasoning and apply a “fix” to a solution. The most exciting part during the journey that has been of special note to me is how students explain a method of solution for an answer. With help from my Teacher Researcher team I started the year with an understanding of the need to have the students be mathematically explicit with a solution. At times it was hard for the students to explain in detail how they reached an answer. In the general course of teaching math we all come across a situation where a student understands what mathematical process needs to be applied, but struggles in the attempt to explain why. Number talks have become an efficient method for working on this skill.
As a team we came up with the idea to have a Guest Recorder. The version I found to be the most fruitful was where one classmate went into the hallway while the number talk was presented and answered. With only the solution(s) listed on the board, the guest was summoned back into the room. The solution strategies were then justified with the guest translating. The charge of the group was to produce an explicit method of solution that would work for all similar problems. Included in this method was a written explanation.

The benefit of this twist on number talks was the increased participation. In the discussion that followed, the students commented that they had to work harder to get their ideas across. This turned into groups of students with similar ideas helping each other explain.
Here is one result when the students had to write the steps to the method.
If possible, get the numerators to be the same.
Multiply fraction #1 by the denominator from fraction #2.
Multiply fraction #2 by the denominator from fraction #1.
Compare the numerators.
The fraction with the larger numerator is the larger fraction.
The requirement was that students use the correct vocabulary and mathematically-sound reasoning. After the students were done with this step, I proceeded to use this same strategy on a new problem as shown below.
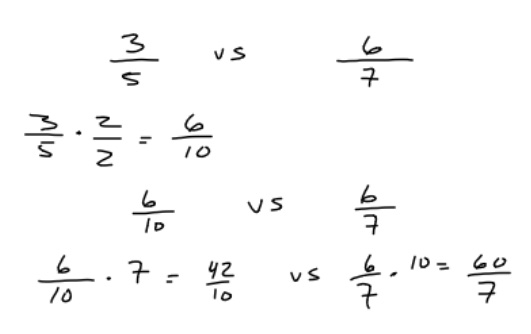
The final result of (42/10 vs. 60/7) did not provide a solution demonstrating which fraction was the larger of the two. This mistake resulted in a rewrite. The students quickly saw the issue with the steps, offered the editing shown below, and a lesson in being precise was learned.

The use of a Guest Recorder raised the level of participation by causing the students to be more precise with the vocabulary they needed to use. It also allowed more group effort as two or three students attempted to get the speaker to write what they intended for a solution.
Team Number Talk
Megann Line, Waukesha, WI megannline@cpm.org
A Team Number Talk is yet another twist to try when facilitating number talks. This is where the students facilitate the number talk within their study teams. Before doing a Team Number Talk, it is important to review the team roles (Task Manager, Facilitator, Recorder/Reporter, and Resource Manager) and to reiterate the jobs and tasks associated with each. This helps the conversations that occur with the number talks to be equitable. This style of a number talk is designed to encourage conversation throughout daily lessons and to help conversations happen naturally. Another way we have noticed this style of number talk to be effective is with students’ precision with vocabulary. Because the students are meeting with their teams they feel less threatened when another classmate corrects their vocabulary. For example, a student might point out when a teammate is calling a multiple a factor or vice versa. After the Team Number Talk, we come together as a whole group to observe different teams’ strategies. Classroom teachers could discuss strategies as a whole group or have teams trade whiteboards, displaying their solutions so teams can discuss them with each other. The most valuable element that we have noticed when students do a Team Number Talk is that students are owning the importance of sharing their strategies even if they have a different solution. Students tend to modify their solution or strategy as they discuss, and go from thinking individually to thinking as a team. This is how ideas are developed together. As teachers, this is what we want to happen with every lesson: cultivation of the ability to think individually and with a team.

Can You Make It?
Angela Kraft, Oconomowoc, WI angelakraft@cpm.org
Another version of a number talk that we decided to try was a Can You Make It? type of problem. For example, can you make 24 using the digits 2, 7, 3, 8, 4, and 6? Students try to create equations using any operations to obtain the targeted value.

We treated this problem the same as any number talk by asking the students to place one fist on their heart and one hand on their desks. During the wait time, students displayed how many different ways they could make the target number with their fingers. This type of number talk offers the same great elements as many other number talks; in particular, it allows an easy entry point for all students to engage and participate, as well as offers opportunities for students to challenge themselves and think creatively. The participation with this type of number talk grew tremendously due to the ease of access as well as the many types of solutions available. Additionally, these types of number talks are great at targeting the use of precision in mathematics and vocabulary by emphasizing the order of operations and the importance of the use of parentheses. We were amazed that a group of 6th graders were able to come up with and share the solutions included above. Students love the creativity these types of number talks offer as well as how the talks help build strong number sense…the heart of number talks!
Throughout our number talk research, we have experimented with many different twists to help increase participation and help students develop effective communication of solutions with increased mathematical vocabulary. We have found the most success with the four strategies outlined above. Our main goal is to have our work with number talks spill over into whole class and team discussions every day. We continue to focus our attention of appropriate vocabulary usage, precision in sharing of strategies, and increasing participation to all students


