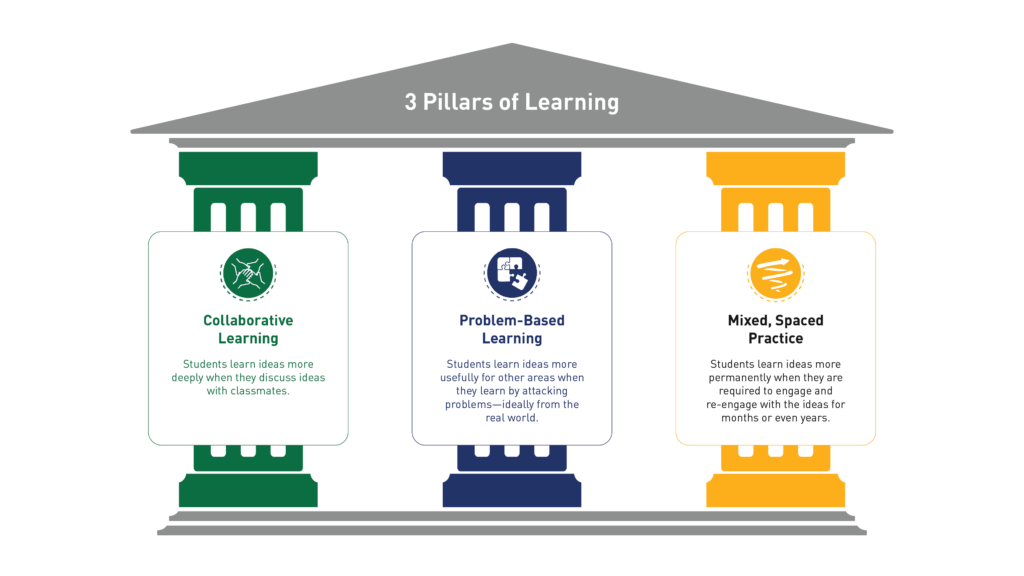
Collaborative Learning: Students learn ideas more deeply when they discuss ideas with classmates.
Problem-Based Learning: Students learn ideas more usefully for other arenas when they learn by attacking problems—ideally from the real world.
Mixed, Spaced Practice: Students learn ideas more permanently when they are required to engage and re-engage with the ideas for months or even years.
These pillars were synthesized from NCTM standards and research on constructivism in the early 1990s. The Three Pillars are still reflected in current NCTM standards and research in mathematics education; what we know about their benefits for mathematics learning continues to deepen and expand but not shift.
CPM curricula are grounded in an extensive and growing research base. This research base includes foundational educational research that supports CPM’s Three Pillars of Collaboration, Problem-Based Learning, and Mixed Spaced Practice.
CPM Educational Program results in meaningful mathematics learning for students and supports teachers to implement high quality instruction aligned with Common Core math content and practice standards.
CPM provides research briefs that synthesize current scholarship on various topics in mathematics education. Research briefs aim to connect parents, teachers, and administrators with research about mathematics education.
Dr. Tom Sallee, a mathematician and co-founder of CPM, reviewed and synthesized the research on mathematics learning in relation to each of The Three Pillars.
Read CPM’s research base reports listed below to learn more about the evidence.
Collaborative Learning is a humanizing way to support students to engage in mathematical practices (i.e., the skills and dispositions necessary to participate in disciplinary discourse) for the production of mathematical knowledge and skills. CPM’s 2024 Report Research Base Collaborative Learning (PDF)
Problem-Based Learning supports students in learning mathematics in ways that will be useful to them in their future mathematics classes, in their careers, and in their lives outside of school and work. When students understand how to solve problems rather than how to correctly select and implement procedures, they develop mathematical authority and thus are more likely to enjoy and see the value in mathematics. CPM’s 2024 Report Research Base Problem-Based Learning (PDF)
Mixed, Spaced Practice supports students in developing mathematical dispositions in which they strive to make sense of problems rather than seek correct answers by mindlessly following procedures. Students will develop procedural fluency as they become increasingly proficient at identifying problem types and selecting appropriate problem-solving strategies. CPM’s 2024 Report Research Base Mixed, Spaced Practice (PDF)
Read about CPM’s impact in these Performance Reports below.
Learn about how the quality of briefs is understanding what quality instruction looks like, how, and why it works.
Research briefs will be prepared at the discretion of CPM’s Research Department.
In the current moment with crisis discourses of “learning loss” and “falling behind,” many teachers are navigating felt tensions between meeting students where they are and maintaining the rigor of their curriculum. Executive Summary — Designing Mathematics Instruction in the Wake of Crisis (PDF)
How can we support students with learning and intellectual disabilities to experience productive struggle during collaborative problem-solving on cognitively-demanding tasks? Executive Summary — Inclusion and Intervention: Understanding “Disability” in the Mathematics Classroom (PDF)
Collaborative and cooperative classrooms have different cultures: the former shaped by practices of inquiry and argumentation and the latter by practices of strategy sharing and reporting. Beyond Cooperation: Building Collaborative Classroom Cultures to Increase Engagement and Rigor (PDF)
CPM’s three-part lesson structure is geared towards supporting students to have agency in and take ownership of their learning. This is quite different from other three-part lesson structures such as the gradual release method of I Do / You Do / We Do. It’s not I Do – We Do – You Do: Understanding the How and Why of CPM’s Three-Part Lessons (PDF)
The Annenberg Institute at Brown University has research briefs focusing on recovery from COVID-19, with overarching topics of student learning, school climate, supporting all students, teachers and leaders, and finances and operations. Annenberg Website
The Answer Lab at the University of Southern California's Rossier School of Education has research briefs focusing on persistent questions of education.
2.3.4
Defining Concavity
4.4.1
Characteristics of Polynomial Functions
5.2.6
Semi-Log Plots
5 Closure
Closure How Can I Apply It? Activity 3
9.3.1
Transition States
9.3.2
Future and Past States
10.3.1
The Parametrization of Functions, Conics, and Their Inverses
10.3.2
Vector-Valued Functions
11.1.5
Rate of Change of Polar Functions
This professional learning is designed for teachers as they begin their implementation of CPM. This series contains multiple components and is grounded in multiple active experiences delivered over the first year. This learning experience will encourage teachers to adjust their instructional practices, expand their content knowledge, and challenge their beliefs about teaching and learning. Teachers and leaders will gain first-hand experience with CPM with emphasis on what they will be teaching. Throughout this series educators will experience the mathematics, consider instructional practices, and learn about the classroom environment necessary for a successful implementation of CPM curriculum resources.
Page 2 of the Professional Learning Progression (PDF) describes all of the components of this learning event and the additional support available. Teachers new to a course, but have previously attended Foundations for Implementation, can choose to engage in the course Content Modules in the Professional Learning Portal rather than attending the entire series of learning events again.
