October 2023

Webster defines “missing the boat” as: “To fail to take advantage of an opportunity.”

Thehagueonline.com explains it further: “The idiom ‘missed the boat’ was once used in a very literal way and is believed to have originated from British English sea slang. As such, the saying referred to arriving too late to take a scheduled voyage by boat as this was the main form of transportation in former times.” Today, if you say that someone has “missed the boat,” you mean that they have failed to take advantage of a good opportunity, or that they are totally ignorant of a situation and have thus made an error in judgment.

In all my years of teaching, I feel like I was missing the boat, until now.

Each school year, I try out a new idea: implementing something I learned over the summer or experimenting mid-year. Several years ago, Rudy Botz and I created THE BOARD REPORT. This strategy created purposeful movement of students and invited mathematical conversations. Paired with Swapmeets, Huddles, and T.I.P.S., it was the best of the four strategies that we used. At the time, Rudy and I thought we were on the boat.

Next, after COVID, THE GOAL OF THE LESSON changed what I do in class forever. I feel it is the heart and soul of what problem-based learning should be. We started each class with a question: “What is the difference between intersections and intercepts?” We used the core problems to investigate and explore this question. At the end of the lesson, we answered the question with pictures and words that summarized our learning. During class, we used all of the strategies listed above to help students make sense of problems and persevere in solving them. At this point, I thought not only was I on the boat, I was starting to get my sea legs.

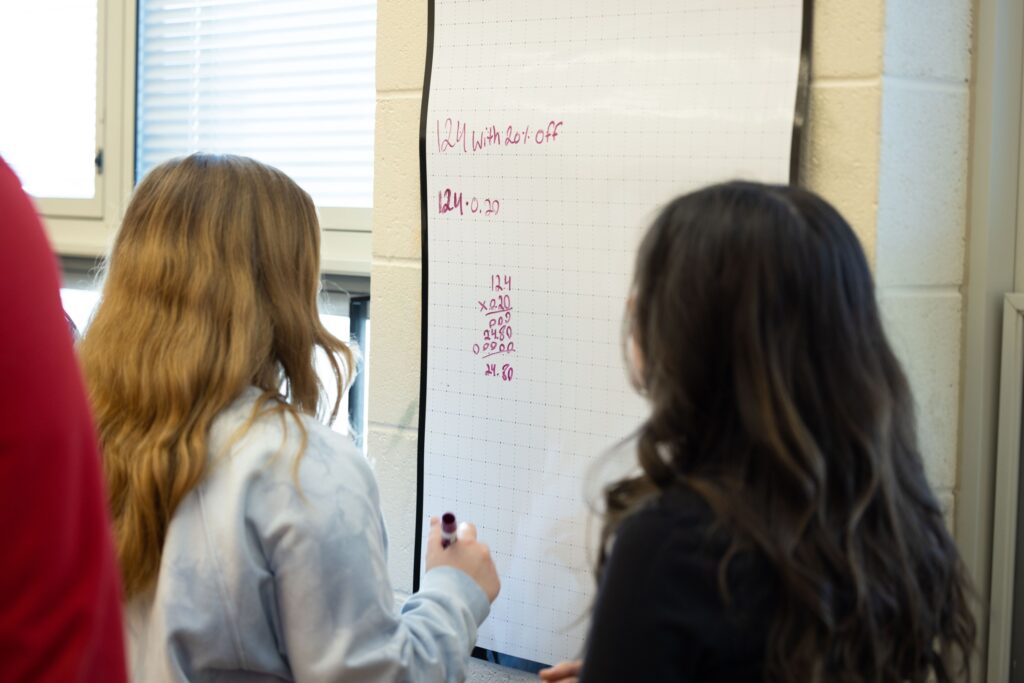
In November of 2021, I read Daniel Henderson’s CPM article WRITE IT UP (ON THE WALL). Henderson wrote: “For years I sensed that something about using VNPS might transform my classes, but failed to fully grasp it. I humbly suggest you also make VNPSs your default work setting.” I remember reading it but not taking action. I failed to fully grasp what it would look like in the classroom or how I would implement it. Looking back, I realize I was missing the boat. Until now.

Regardless of the course, there is no limit to problems that need to be solved up on the wall. It is remarkable what happens in class when students can see what other teams are thinking. Students come into the room telling me that they hope we are working on whiteboards that day. They are much more likely to take risks and make mistakes.

 

When we work vertically, our most typical workflow involves the 4-person, 4-marker challenge or 2up/2down. The 4-person, 4-marker challenge means that everyone on the team gets a different color marker. The challenge is to have each person contribute thinking towards a particular problem. Teams sit when they are finished and we debrief as a class: we look for multiple solving methods and celebrate teams who were able to incorporate each color (person). 2up/2down means that two students go to the whiteboard and two students remain seated. The students standing work the problem as a pair and the students sitting work it individually. They can use the rest of the whiteboards for hints or tips to start the problem. When the standing students are finished, they “tag in” (WWE reference) the other two team members and switch spots. They sit down, and the others get up.

It is not perfect, and I am still learning as I go, but you can tell a difference in our mathematical conversations and confidence. It feels like a new wave of mathematics. Maybe it is because I am finally on the boat.